- 2021-06-16 发布 |
- 37.5 KB |
- 24页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高中数学选修2-2教学课件第1课时 几个常用函数的导数与基本初等函数的导数公式
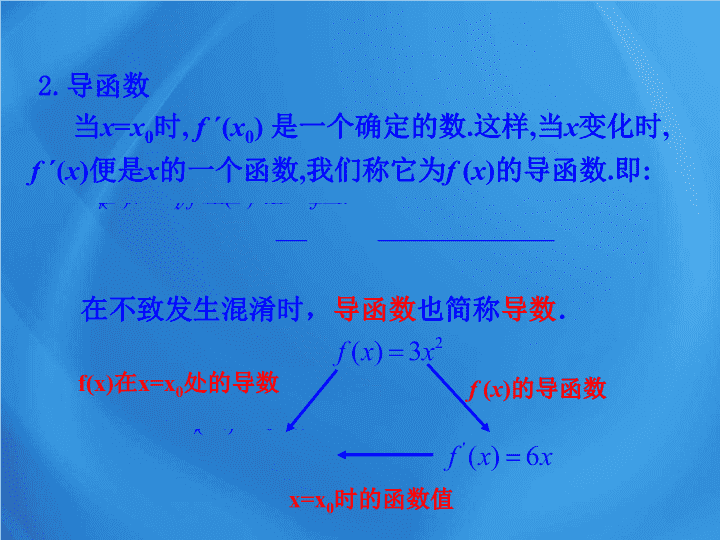
1.2 导数的计算 第 1 课时 几个常用函数的导数 与基本初等函数的导数公式 1. 求函数在点 x 0 处的导数的方法是 : 在不致发生混淆时, 导函数 也简称 导数 . 2. 导函数 当 x = x 0 时 , f ´ ( x 0 ) 是一个确定的数 . 这样 , 当 x 变化时 , f ´( x ) 便是 x 的一个函数 , 我们称它为 f ( x ) 的导函数 . 即 : f(x) 在 x=x 0 处的导数 f ( x ) 的导函数 x=x 0 时的函数值 1. 能利用导数的定义推导函数 y = c , y = x , y = x 2 , y = x -1 , y = 的导数 . 2. 能根据基本初等函数的求导公式,求简单 函数的导数. (重点) 探究点 1 几种常见函数的导数 根据导数的定义可以得出一些常见函数的导数公式 . 公式一 : 1. 函数 y=f(x)=c 的导数 . 2. 函数 y=f(x)=x 的导数 3. 函数 y=f(x)=x 2 的导数 探究点 2 基本初等函数的导数公式 ( 1 )若 f ( x )=c(c 为常数 ), 则 = ; ( 2 )若 f ( x )= x a ( a ∈Q * ), 则 = ; ( 3 )若 f ( x )=sin x , 则 = ; ( 4 )若 f ( x )= cos x , 则 = ; ( 5 )若 f ( x )= a x , 则 = ; a x ln a cos x -sin x 0 ( 6 )若 f ( x )=e x , 则 f′ ( x )=_____; ( 7 )若 f ( x )=log a x , 则 f′ ( x )=_______; ( 8 )若 f ( x )=ln x , 则 f ′ ( x )=______. e x 【 变式练习 】 例 2 求下列函数的导数 ( 1 ) y=a 2 (a 为常数 ). ( 2 ) y=x 12 . ( 3 ) y=x -4 . ( 4 ) y=lg x. 【 总结提升 】 (1) 用导数的定义求导是求导数的基本方法,但运算较繁.利用常用函数的导数公式,可以简化求导过程,降低运算难度. (2) 利用导数公式求导,应根据所给问题的特征,恰当地选择求导公式,将题中函数的结构进行调整.如将根式、分式转化为指数式,利用幂函数的求导公式求导. 在确定与切线垂直的直线方程时,应注意考察函数在切点处的导数 y ′ 是否为零,当 y ′ = 0 时,切线平行于 x 轴,过切点 P 垂直于切线的直线斜率不存在. 【 总结提升 】 1. 选择题 ( 1 )下列各式正确的是 ( ) C ( 2 )下列各式正确的是( ) D (1) f(x)=80 ,则 f ′ (x)=______; 2. 填空 0 e+1 (5) 曲线 y = x n 在 x = 2 处的导数为 12 ,则 n 等于 ____ . 3 2. 基本初等函数的导数公式 ( 1 )若 f (x)=c, 则 f ′ (x)=____; ( 2 )若 f (x)=x a (a∈ Q * ), 则 f ′ (x)= ; ( 3 )若 f (x)=sin x, 则 f ′ (x)=______; ( 4 )若 f (x)= cos x, 则 f ′ (x)=_______; ( 5 )若 f (x)=a x , 则 f ′ (x)=__________; a x ln a cos x -sin x 0 1. 会求常用函数的导数 . a x a -1 ( 6 )若 f (x)=e x , 则 f ′ (x)=____; ( 7 )若 f (x)=log a x, 则 f ′ (x)= ; ( 8 )若 f (x)=ln x, 则 f ′ (x)=____. e x 业精于勤,荒于嬉;行成于思,毁于随 . —— 韩愈查看更多