- 2021-06-16 发布 |
- 37.5 KB |
- 33页


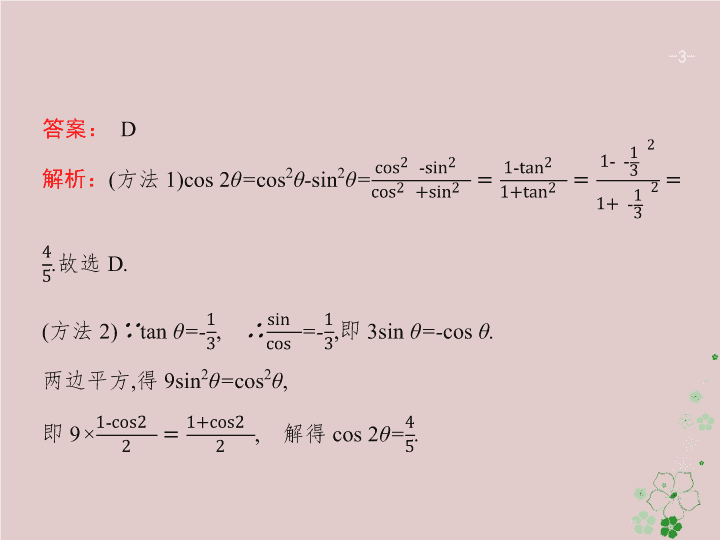
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2018届二轮复习三角变换与解三角形课件文(全国通用)
3.2 三角变换与解三角形 -2- 热点1 热点2 热点3 热点4 -3- -4- 热点1 热点2 热点3 热点4 题后反思从函数名、角、运算三方面进行差异分析,变换的基本 思路是:异角化同角,异名化同名,高次化低次;常用的技巧是:切化弦、 降幂公式、用三角公式转化出现特殊角. -5- 热点1 热点2 热点3 热点4 -6- -7- 热点1 热点2 热点3 热点4 -8- -9- 热点1 热点2 热点3 热点4 -10- 热点1 热点2 热点3 热点4 -11- -12- 热点1 热点2 热点3 热点4 -13- -14- 热点1 热点2 热点3 热点4 题后反思关于解三角形问题,一般要用到三角形内角和定理、正弦 定理、余弦定理及有关三角形的性质,常见的三角变换方法和原则 都适用.同时,要注意“三统一”,即“统一角、统一函数、统一结构”, 这是使问题获得解决的突破口. -15- 热点1 热点2 热点3 热点4 -16- -17- -18- 热点1 热点2 热点3 热点4 -19- -20- 热点1 热点2 热点3 热点4 题后反思对于一个解三角形的综合问题,若条件是既有边又有角的 关系式,在进行运算时有两种方法:一是先应用正弦定理把边转化 为角,再利用三角恒等变换进行化简整理;二是先应用余弦定理把 角转化为边,再进行字母的代数运算,使关系式得到简化. -21- 热点1 热点2 热点3 热点4 -22- 1.三角恒等变形的基本思路: (1)“化异名为同名”“化异次为同次”“化异角为同角”; (2)“切化弦”“1”的代换; (3)角的变换是三角变换的核心,如β=(α+β)-α,2α=(α+β)+(α-β)等. 2.倍角、半角公式应用的技巧:公式的正用、逆用和变形用. 3.在处理三角形中的边角关系时,一般全部化为角的关系,或全部化 为边的关系.题中若出现边的一次式一般采用到正弦定理,出现边 的二次式一般采用到余弦定理.正弦定理的形式多样,其中a=2Rsin A,b=2Rsin B,c=2Rsin C能够实现边角互化. 4.在解三角形中,三角形内角和定理起着重要作用,在解题中要注意 根据这个定理确定角的范围,确定三角函数值的符号,防止出现增 解等扩大范围的现象. -23- -24- -25- -26- -27- -28- -29- -30- -31- -32- -33-查看更多