2021版高考数学一轮复习核心素养测评九函数的图象苏教版
核心素养测评九 函数的图象
(25分钟 50分)
一、选择题(每小题5分,共35分)
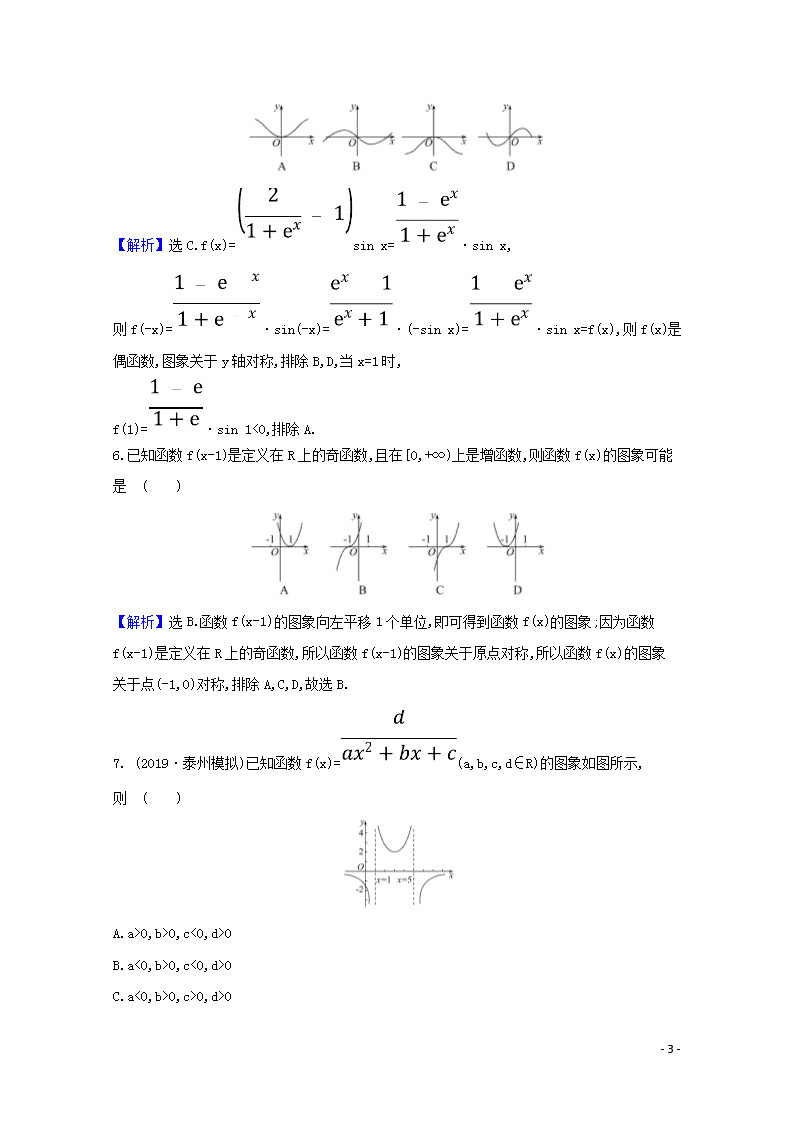
1.(2020·长沙模拟)函数f(x)=的大致图象是 ( )
【解析】选D.函数f(x)=是偶函数,排除选项B,当x=2时,f(2)=-<0,对应点在第四象限,排除A,C.
2.已知函数f(x)的图象如图所示,则f(x)的解析式可以是 ( )
A.f(x)= B.f(x)=
C.f(x)=-1 D.f(x)=x-
- 10 -
【解析】选A.由函数图象可知,函数f(x)为奇函数,应排除B,C;若函数的解析式为f(x)=x-,则当x→+∞时,f(x)→+∞,排除D.
3.函数f(x)=(e是自然对数的底数)的图象 ( )
A.关于x轴对称
B.关于y轴对称
C.关于原点对称
D.关于直线y=x对称
【解析】选B.因为f(x)=ex+e-x,所以f(x)为偶函数,图象关于y轴对称.
4.如图,函数f(x)的图象为折线ACB,则不等式f(x)≥log2(x+1)的解集是( )
A.{x|-1
0,b>0,c<0,d>0
B.a<0,b>0,c<0,d>0
C.a<0,b>0,c>0,d>0
- 10 -
D.a>0,b<0,c>0,d>0
【解析】选B.由题图可知,x≠1且x≠5,则ax2+bx+c=0的两根为1,5,
由根与系数的关系,得-=6,=5,
所以a,b异号,a,c同号,又f(0)=<0,所以c,d异号,只有B项适合.
【变式备选】
已知函数y=f(-|x|)的图象如图所示,则函数y=f(x)的图象不可能是 ( )
【解析】选C.函数y=f(-|x|)=
当x<0时,y=f(-|x|)=f(x),
所以函数y=f(-|x|)的图象在y轴左边的部分,就是函数y=f(x)的图象,故可得函数y=f(x)的图象不可能是C.
二、填空题(每小题5分,共15分)
8.不等式log2(-x)0时,函数f(x)在R上是单调增函数;
②当b<0时,函数f(x)在R上有最小值;
③函数f(x)的图象关于点(0,c)对称;
④方程f(x)=0可能有三个实数根.
【解析】f(x)=
结合图象(图略)可知①正确,②不正确,对于③,因为y=|x|x+bx是奇函数,其图象关于原点(0,0)对称,所以f(x)的图象关于点(0,c)对称,③正确;
当c=0,b<0时f(x)=0有三个实数根,故④正确.
答案:①③④
(15分钟 35分)
1.(5分)(2020·潍坊模拟)如图所示的函数图象,对应的函数解析式可能
是 ( )
A.y=2x-x2-1 B.y=2xsin x
C.y= D.y=(x2-2x)ex
【解析】选D.因为y=2xsin x为偶函数,其图象关于y轴对称,所以排除B.
- 10 -
因为函数y=的定义域为{x|01},所以排除C.
对于y=2x-x2-1,
当x=-2时,y=2-2-(-2)2-1<0,所以排除A.
2.(5分) (2020·淮安模拟)若直角坐标系内A,B两点满足:
(1)点A,B都在f(x)图象上;(2)点A,B关于原点对称,则称点对(A,B)是函数f(x)的一个“和谐点对”,(A,B)与(B,A)可看作一个“和谐点对”.已知函数f(x)=则f(x)的“和谐点对”有 ( )
A.1个 B.2个 C.3个 D.4个
【解析】选B.作出函数y=x2+2x(x<0)的图象关于原点对称的图象(如图中的虚线部分),
看它与函数y=(x≥0)的图象的交点个数即可,观察图象可得交点个数为2,即f(x)的“和谐点对”有2个.
【变式备选】
(2019·北师大附中模拟)函数y=ecos x(-π≤x≤π)的大致图象为 ( )
【解析】选C.显然,该函数为偶函数,
当x=0时,函数y取得最大值ecos 0=e;
当x=π时,y=ecos π=;
- 10 -
当x=-π时,y=ecos(-π)=.
可排除A,B,D.
3.(5分)对于函数f(x)=lg(|x-2|+1),给出如下三个结论:
①f(x+2)是偶函数;②f(x)在区间(-∞,2)上是减函数,在区间(2,+∞)上是增函数;③f(x)没有最小值.其中正确的序号是________.
【解析】作出f(x)的图象,可知f(x)在(-∞,2)上是减函数,在(2,+∞)上是增函数;
由图象可知函数存在最小值0.所以①②正确.
答案:①②
【变式备选】
已知a>0,函数f(x)=若关于x的方程f(x)=ax恰有2个互异的实数解,则a的取值范围是________.
【解析】由题可设函数g(x)=f(x)-ax=
当x≤0时,Δ1=a2-4a,当x>0时,
Δ2=a2-8a.根据题目条件可知a>0时,
函数g(x)恰有2个不同的零点,可分以下三种情况:
①当时,解得a=0,不满足条件a>0,此时无解;
②当时,解得40在R上恒成立,求m的取值范围.
【解析】(1)令F(x)=|f(x)-2|=|2x-2|,G(x)=m,画出F(x)的图象如图所示.
由图象可知,当m=0或m≥2时,
函数F(x)与G(x)的图象只有一个交点,原方程有一个解;
- 10 -
当00),H(t)=t2+t,
因为H(t)=-在区间(0,+∞)上是增函数,所以H(t)>H(0)=0.
因此要使t2+t>m在区间(0,+∞)上恒成立,应有m≤0,即所求m的取值范围为
(-∞,0].
【变式备选】
已知a∈R,函数f(x)=+a在[1,4]上的最大值是5,求a的取值范围.
【解析】因为x∈[1,4],所以x+∈[4,5],
当a≥5时,f(x)=a-x-+a=2a-x-,
所以f(x)的最大值为2a-4=5,a=与a≥5矛盾,舍去,
当a≤4时,f(x)=x+-a+a=x+≤5,此时命题成立.
当4
查看更多