【数学】2019届一轮复习人教A版 几何证明选讲 作业

【数学】2019届一轮复习人教A版 几何证明选讲 作业

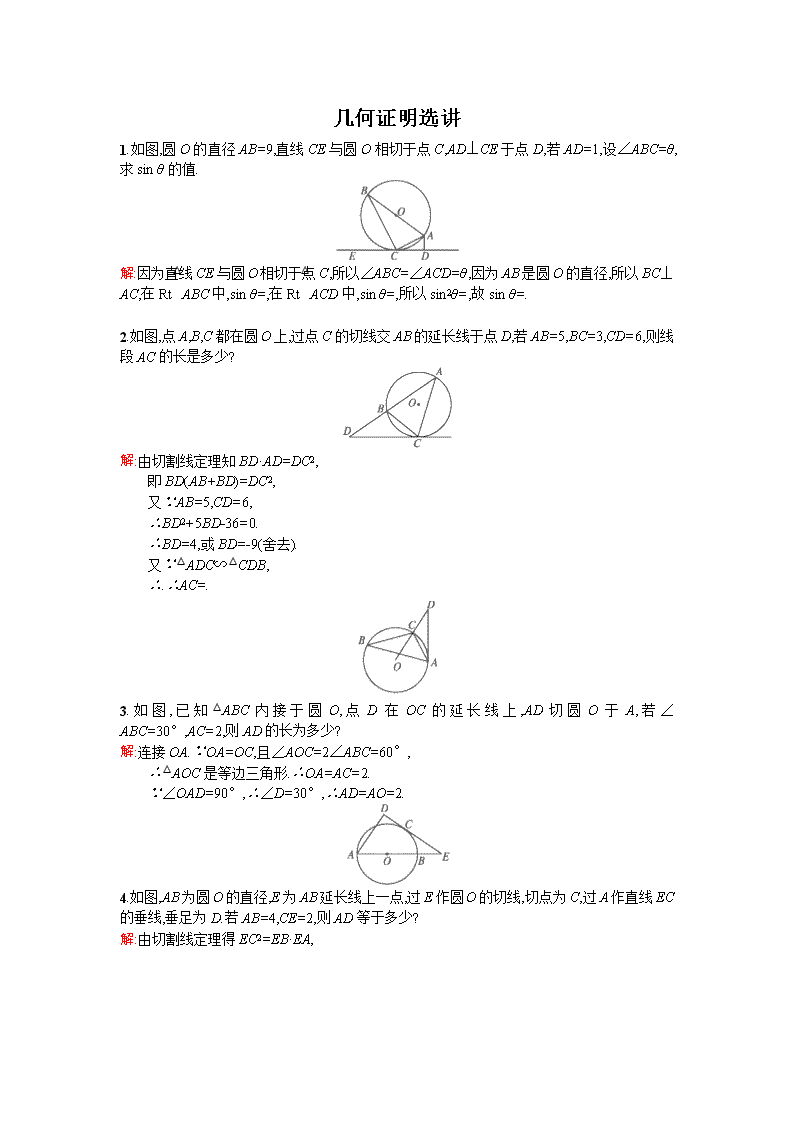
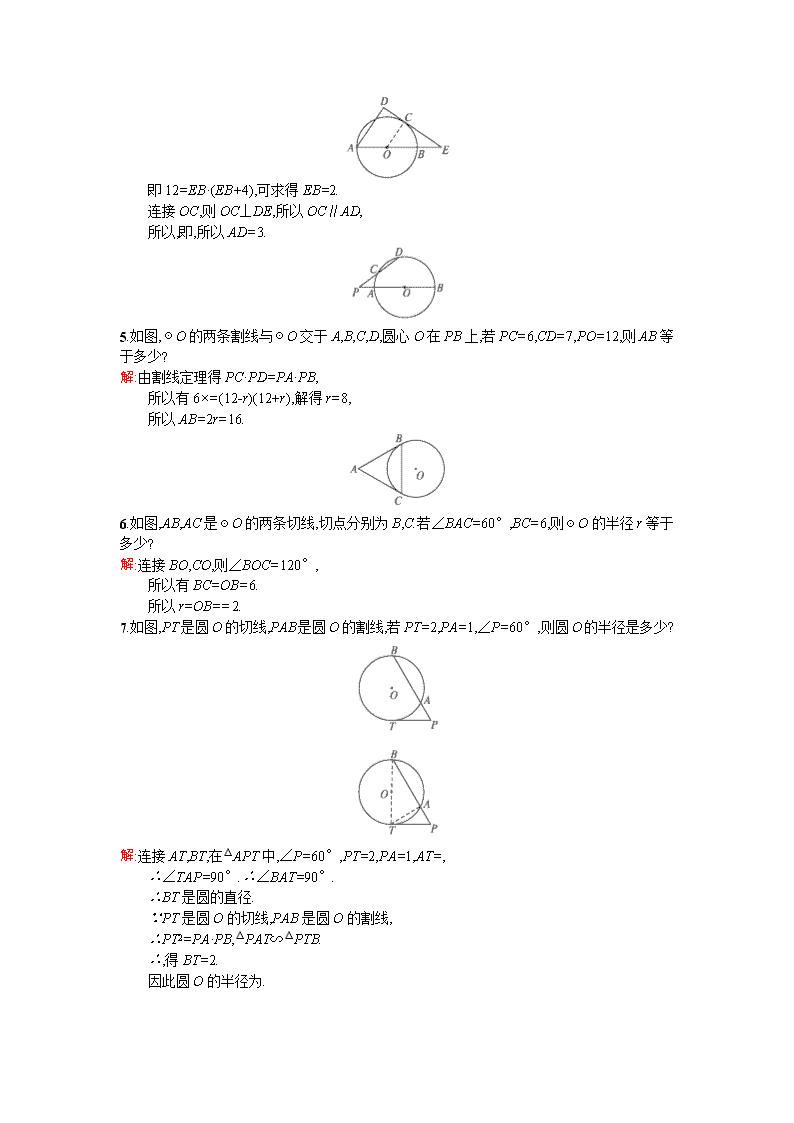
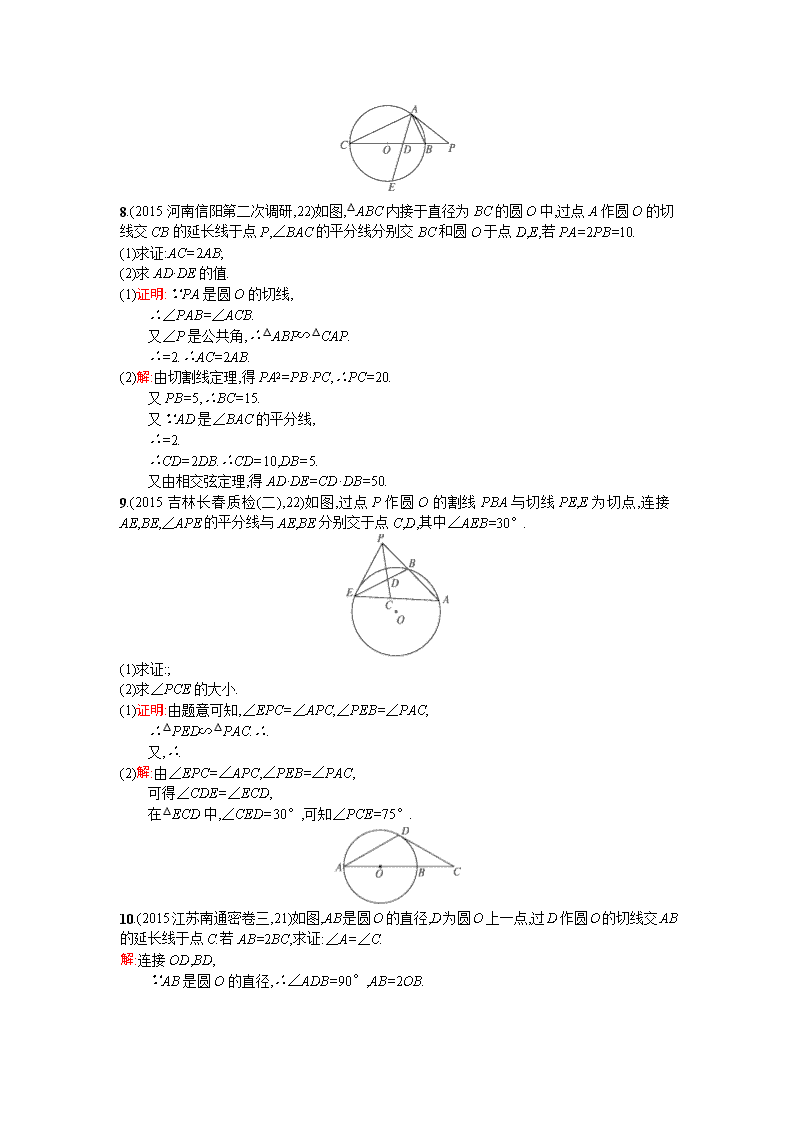
几何证明选讲 ‎1.如图,圆O的直径AB=9,直线CE与圆O相切于点C,AD⊥CE于点D,若AD=1,设∠ABC=θ,求sin θ的值.‎ ‎ ‎ 解:因为直线CE与圆O相切于点C,所以∠ABC=∠ACD=θ,因为AB是圆O的直径,所以BC⊥AC,在Rt△ABC中,sin θ=,在Rt△ACD中,sin θ=,所以sin2θ=,故sin θ=.‎ ‎ ‎ ‎2.如图,点A,B,C都在圆O上,过点C的切线交AB的延长线于点D,若AB=5,BC=3,CD=6,则线段AC的长是多少?‎ ‎ ‎ 解:由切割线定理知BD·AD=DC2,‎ 即BD(AB+BD)=DC2,‎ 又∵AB=5,CD=6,‎ ‎∴BD2+5BD-36=0.‎ ‎∴BD=4,或BD=-9(舍去).‎ 又∵△ADC∽△CDB,‎ ‎∴.∴AC=.‎ ‎ ‎ ‎3.如图,已知△ABC内接于圆O,点D在OC的延长线上,AD切圆O于A,若∠ABC=30°,AC=2,则AD的长为多少?‎ 解:连接OA.∵OA=OC,且∠AOC=2∠ABC=60°,‎ ‎∴△AOC是等边三角形.∴OA=AC=2.‎ ‎∵∠OAD=90°,∴∠D=30°,∴AD=AO=2.‎ ‎ ‎ ‎4.如图,AB为圆O的直径,E为AB延长线上一点,过E作圆O的切线,切点为C,过A作直线EC的垂线,垂足为D.若AB=4,CE=2,则AD等于多少?‎ 解:由切割线定理得EC2=EB·EA,‎ ‎ ‎ 即12=EB·(EB+4),可求得EB=2.‎ 连接OC,则OC⊥DE,所以OC∥AD,‎ 所以,即,所以AD=3.‎ ‎ ‎ ‎5.如图,☉O的两条割线与☉O交于A,B,C,D,圆心O在PB上,若PC=6,CD=7,PO=12,则AB等于多少?‎ 解:由割线定理得PC·PD=PA·PB,‎ 所以有6×=(12-r)(12+r),解得r=8,‎ 所以AB=2r=16.‎ ‎ ‎ ‎6.如图,AB,AC是☉O的两条切线,切点分别为B,C.若∠BAC=60°,BC=6,则☉O的半径r等于多少?‎ 解:连接BO,CO,则∠BOC=120°,‎ 所以有BC=OB=6.‎ 所以r=OB==2.‎ ‎7.如图,PT是圆O的切线,PAB是圆O的割线,若PT=2,PA=1,∠P=60°,则圆O的半径是多少?‎ ‎ ‎ ‎ ‎ 解:连接AT,BT,在△APT中,∠P=60°,PT=2,PA=1,AT=,‎ ‎∴∠TAP=90°.∴∠BAT=90°.‎ ‎∴BT是圆的直径.‎ ‎∵PT是圆O的切线,PAB是圆O的割线,‎ ‎∴PT2=PA·PB,△PAT∽△PTB.‎ ‎∴,得BT=2.‎ 因此圆O的半径为.‎ ‎ ‎ ‎8.(2015河南信阳第二次调研,22)如图,△ABC内接于直径为BC的圆O中,过点A作圆O的切线交CB的延长线于点P,∠BAC的平分线分别交BC和圆O于点D,E,若PA=2PB=10.‎ ‎(1)求证:AC=2AB;‎ ‎(2)求AD·DE的值.‎ ‎(1)证明:∵PA是圆O的切线,‎ ‎∴∠PAB=∠ACB.‎ 又∠P是公共角,∴△ABP∽△CAP.‎ ‎∴=2.∴AC=2AB.‎ ‎(2)解:由切割线定理,得PA2=PB·PC,∴PC=20.‎ 又PB=5,∴BC=15.‎ 又∵AD是∠BAC的平分线,‎ ‎∴=2.‎ ‎∴CD=2DB.∴CD=10,DB=5.‎ 又由相交弦定理,得AD·DE=CD·DB=50.‎ ‎9.(2015吉林长春质检(二),22)如图,过点P作圆O的割线PBA与切线PE,E为切点,连接AE,BE,∠APE的平分线与AE,BE分别交于点C,D,其中∠AEB=30°.‎ ‎ ‎ ‎(1)求证:;‎ ‎(2)求∠PCE的大小.‎ ‎(1)证明:由题意可知,∠EPC=∠APC,∠PEB=∠PAC,‎ ‎∴△PED∽△PAC.∴.‎ 又,∴.‎ ‎(2)解:由∠EPC=∠APC,∠PEB=∠PAC,‎ 可得∠CDE=∠ECD,‎ 在△ECD中,∠CED=30°,可知∠PCE=75°.‎ ‎ ‎ ‎10.(2015江苏南通密卷三,21)如图,AB是圆O的直径,D为圆O上一点,过D作圆O的切线交AB的延长线于点C.若AB=2BC,求证:∠A=∠C.‎ 解:连接OD,BD,‎ ‎∵AB是圆O的直径,∴∠ADB=90°,AB=2OB.‎ ‎ ‎ ‎∵AB=2BC,∴AB=OC.‎ ‎∵DC是圆O的切线,∴∠CDO=90°.‎ ‎∵OB=BC,∴BD=OC.‎ ‎∵OA=OB,∴OD=AB.∴BD=OD.‎ ‎∴△ADB≌△CDO.∴AD=DC,∴∠A=∠C.‎ ‎11.(2015甘肃天水一轮检测,22)如图,AB是☉O的直径,AC是弦,∠BAC的平分线AD交☉O于D,DE⊥AC交AC延长线于点E,OE交AD于点F.‎ ‎ ‎ ‎(1)求证:DE是☉O的切线;‎ ‎(2)若,求的值.‎ ‎(1)证明:连接OD,可得∠ODA=∠OAD=∠DAC,‎ ‎∴OD∥AE.‎ ‎ ‎ 又AE⊥DE,∴OD⊥DE.‎ ‎∴DE是☉O的切线.‎ ‎(2)解:过D作DH⊥AB于H,则有∠DOH=∠CAB,‎ ‎∴cos ∠DOH=cos ∠CAB=.‎ 设OD=5x,则OH=3x,‎ ‎∴AH=8x.‎ 由△ADE≌△ADH,可得AE=AH=8x,‎ 又△AEF∽△DOF,∴.‎ ‎ ‎