云南省曲靖市罗平县第一中学2019-2020学年高二上学期期中考试数学(文)试卷
数学试卷(文科)
一、选择题.
1.从某班65名同学中选取6名组成一个志愿者团,若采用下面的方法选取:先用简单随机抽样从65人中剔除5人,余下的60人再按系统抽样的方法进行,则每人入选的机会
A.不全相等 B.均不相等
C.都相等 D.无法确定
2.先后抛掷两颗骰子,设出现的点数之和是5,6,7的概率依次是P1,P2,P3,则
A.P1=P3
1或x<-1,则x2>1 D.若x≥1或x≤-1,则x2≥1
4.已知命题p:在△ABC中,若A>B,则cos A>cos B,则下列命题为真命题的是
A.p的逆命题 B.p的否命题
C.p的逆否命题 D.p的否定
5.当x=2时,下面的程序段结果是
A.3 B.7
C.15 D.17
6.如图所示是一样本的频率分布直方图,则由图形中的
数据,可以估计众数与中位数分别是
A.12.5 12.5
B.12.5 13
C.13 12.5
D.13 13
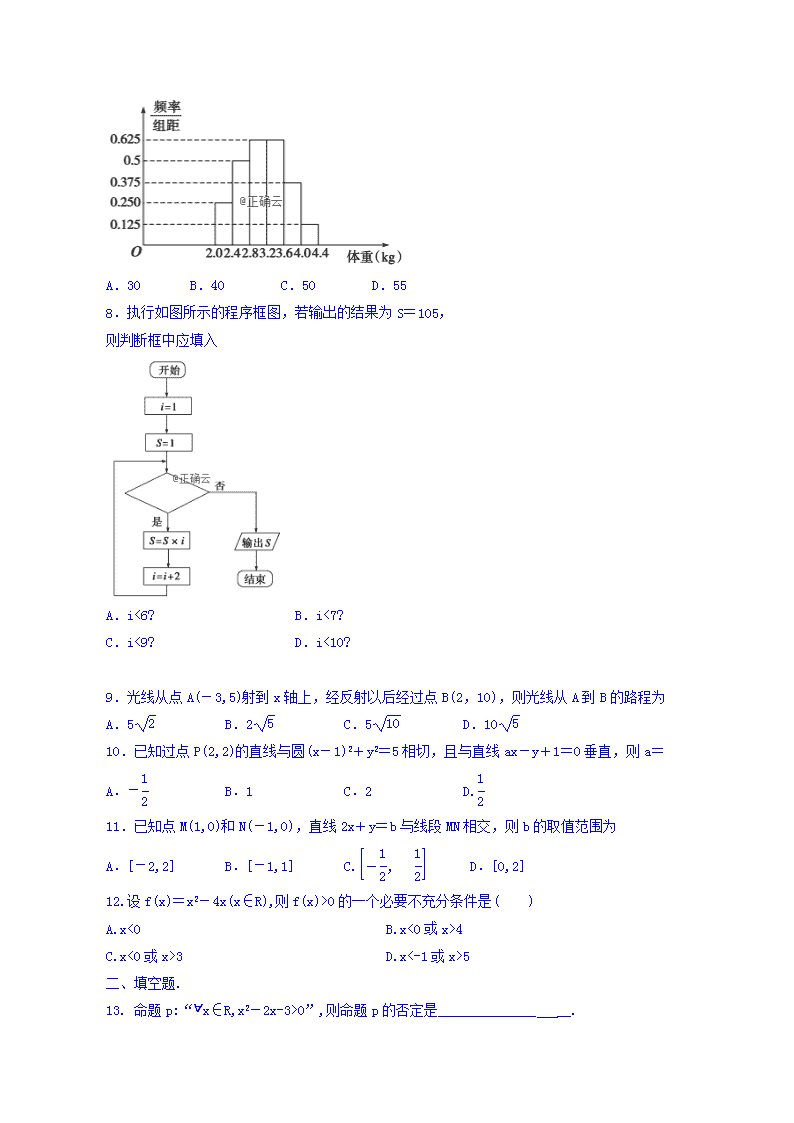
7.某调查机构调查了某地100个新生婴儿的体重,并根据所得数据画出了样本的频率分布直方图(如图所示),则新生婴儿的体重(单位:kg)在[3.2,4.0)的人数是
A.30 B.40 C.50 D.55
8.执行如图所示的程序框图,若输出的结果为S=105,
则判断框中应填入
A.i<6? B.i<7?
C.i<9? D.i<10?
9.光线从点A(-3,5)射到x轴上,经反射以后经过点B(2,10),则光线从A到B的路程为
A.5 B.2 C.5 D.10
10.已知过点P(2,2)的直线与圆(x-1)2+y2=5相切,且与直线ax-y+1=0垂直,则a=
A.- B.1 C.2 D.
11.已知点M(1,0)和N(-1,0),直线2x+y=b与线段MN相交,则b的取值范围为
A.[-2,2] B.[-1,1] C. D.[0,2]
12.设f(x)=x2-4x(x∈R),则f(x)>0的一个必要不充分条件是( )
A.x<0 B.x<0或x>4
C.x<0或x>3 D.x<-1或x>5
二、填空题.
13. 命题p:“∀x∈R,x2-2x-3>0”,则命题p的否定是______________ __.
14.若点P(1,1)为圆x2+y2-6x=0的弦MN的中点,则弦MN所在直线的方程为
15.甲、乙、丙三人进行传球练习,共传球二次,球首先从甲手中传出,则第2
次球恰好传回给甲的概率是________.
16.设点M(x0,1),若在圆O:x2+y2=1上存在点N,使得∠OMN=45°,则x0的取
值范围是_______ _.
三.解答题(17题10分,18-22题均为12分)
17.甲乙两人玩一种游戏,每次由甲、乙各出1到5根手指,若和为偶数算甲赢,否则算乙赢.
(1)若以A表示和为6的事件,求P(A);
(2)这种游戏规则公平吗?试说明理由.
18.已知p:实数x满足x2-4ax+3a2<0,其中a<0;q:实数x满足x2-x-6≤0.若﹁p是﹁q的必要条件,求实数a的取值范围.
19.随机抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图所示.
(1)计算甲班的样本方差;
(2)现从乙班这10名同学中随机抽取两名身高不低于173 cm的同学,求身高176 cm的同学被抽中的概率.
20.过点P(-3,4)的直线l与x轴负半轴y轴正半轴分别交于A,B两点.
(1)求|OA|+|OB|的最小值,并求出此时l的方程.
(2)求面积的最小值,并求出此时l的方程.
21.已知圆C: x2+y2+2x-4y+1=0,O为坐标原点,动点P在圆C外,过P(1,3)作圆C的切线.
(1)切线l的方程;
(2)已知Q(4,0), M为圆C上一动点,求面积的最大值
22.假设关于某设备的使用年限x(年)和所支出的维修费用y(万元)有如下的统计资料:
x
2
3
4
5
6
y
2.2
3.8
5.5
6.5
7.0
(1)求回归直线方程;
(2)估计使用年限为10年时,维修费用是多少?
参考答案
一.1C;2A;3D;4D;5C;6B;7B;8C;9C;10C;11A;12D
二.13, 14,2x-y-1=0 15, 16,[-1,1]
17.解 (1)甲、乙出手指都有5种可能,因此基本事件的总数为5×5=25,事件A包括甲、乙出的手指的情况有(1,5)、(5,1)、(2,4)、(4,2)、(3,3)共5种情况,∴P(A)==.
(2)这种游戏规则不公平.由(1)知和为偶数的基本事件数为13个.(1,1),(1,3),(1,5),(2,2),(2,4),(3,1),(3,3),(3,5),(4,2),(4,4),(5,1),(5,3),(5,5).所以甲赢的概率为,乙赢的概率为.所以这种游戏规则不公平.
18.解:由x2-4ax+3a2<0且a<0得3a<x<a,
所以p:3a<x<a,对应集合A={x|3a<x<a}.
由x2-x-6≤0得-2≤x≤3,
所以q:-2≤x≤3,对应集合B={x|-2≤x≤3}.
因为﹁q⇒﹁p,所以p⇒q,所以A⊆B,
所以⇒-≤a<0, 所以a的取值范围是.
19.解 (1)==170.
甲班的样本方差s2=[(158-170)2+(162-170)2+(163-170)2+(168-170)2+(168-170)2+(170-170)2+(171-170)2+(179-170)2+(179-170)2+(182-170)2]=57.2.
(2)设身高为176 cm的同学被抽中的事件为A,从乙班10名同学中抽中两名身高不低于173 cm的同学有:(181,173),(181,176),(181,178),(181,179),(179,173),(179,176),(179,178),(178,173),(178,176),(176,173)共10个基本事件,而事件A含有4个基本事件:(181,176),(179,176),(178,176),(176,173),∴P(A)==.
20.解:由题意可设l:y-4=k(x+3)(k>0)
x=0时得B(0,3k+4) y=0时得A()
(1) |OA|+|OB|=3k+4++3
所以|OA|+|OB|的最小值
此时3k=解得
l:+12=0
(2)
=24+
=24
所以的面积最小值为24
此时 解得k=
所以l:4x-3y+24=0
21解:把圆C的方程化为标准方程为(x+1)2+(y-2)2=4,
∴圆心为C(-1,2),半径r=2.
(1)当l的斜率不存在时,此时l的方程为x=1,C到l的距离d=2=r,满足条件.
当l的斜率存在时,设斜率为k,得l的方程为y-3=k(x-1),
即kx-y+3-k=0,
则=2,解得k=-.
∴l的方程为y-3=-(x-1),
即3x+4y-15=0.
综上,满足条件的切线l的方程为x=1或3x+4y-15=0.
(2) |PQ|=3
直线PQ的方程为:x+y-4=0
点C到直线PQ的距离为:d=
所以 M到直线PQ的距离的最大值为d+r=
所以 的最大值为
22.解 (1)列表如下:
i
1
2
3
4
5
xi
2
3
4
5
6
yi
2.2
3.8
5.5
6.5
7.0
xiyi
4.4
11.4
22.0
32.5
42.0
=4,=5,=90,iyi=112.3
计算得: ===1.23,
于是: =- =5-1.23×4=0.08,
即得回归直线方程为 =1.23x+0.08.
(2)把x=10代入回归方程 =1.23x+0.08得 =12.38,
因此,估计使用10年维修费用是12.38万