- 2021-06-15 发布 |
- 37.5 KB |
- 12页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2017-2018学年黑龙江省哈尔滨市第六中学高二上学期期中考试数学(理)试题(解析版)
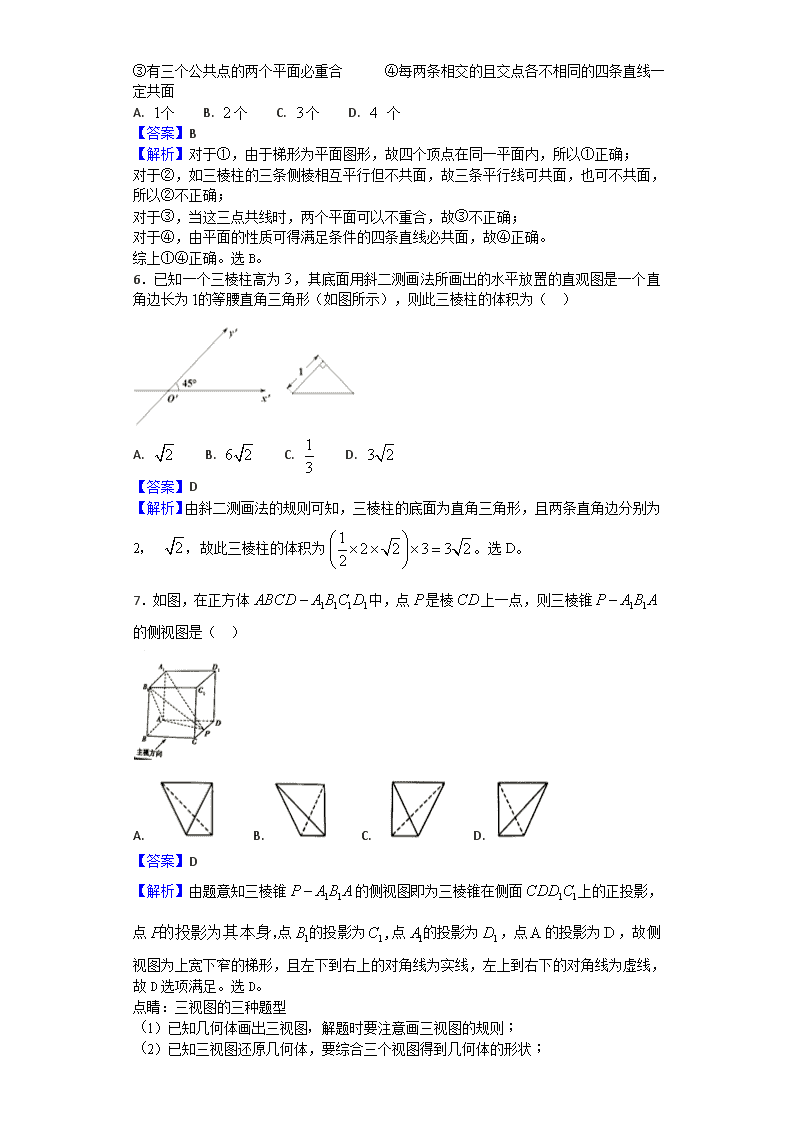
2017-2018学年黑龙江省哈尔滨市第六中学高二上学期期中考试数学(理)试题 一、单选题 1.已知命题,,那么是( ) A. B. C. D. 【答案】C 【解析】由特称命题的否定知,命题“,”的否定为“”。选C。 2.已知双曲线(, )的离心率,则它的渐进线方程为( ) A. B. C. D. 【答案】A 【解析】由得双曲线的渐近线方程为。因为 ,解得,故双曲线的渐近线方程为。选A。 3.在命题“若,则”的逆命题、否命题、逆否命题中,假命题的个数是( ) A. 个 B. 个 C. 个 D. 0 个 【答案】C 【解析】原命题“若,则”为假命题,其逆命题为“若,则”,也为假命题,故原命题的逆命题、否命题、逆否命题都为假命题,即假命题的个数为3。选C。 4.下列几何体中轴截面是圆面的是( ) A. 圆柱 B. 圆锥 C. 球 D. 圆台 【答案】C 【解析】圆柱的轴截面为矩形,圆锥的轴截面为等腰三角形,球的轴截面为圆,圆台的轴截面为等腰梯形。故选C。 5.下列命题正确的个数是( ) ①梯形的四个顶点在同一平面内 ②三条平行直线必共面 ③有三个公共点的两个平面必重合 ④每两条相交的且交点各不相同的四条直线一定共面 A. 个 B. 个 C. 个 D. 个 【答案】B 【解析】对于①,由于梯形为平面图形,故四个顶点在同一平面内,所以①正确; 对于②,如三棱柱的三条侧棱相互平行但不共面,故三条平行线可共面,也可不共面,所以②不正确; 对于③,当这三点共线时,两个平面可以不重合,故③不正确; 对于④,由平面的性质可得满足条件的四条直线必共面,故④正确。 综上①④正确。选B。 6.已知一个三棱柱高为,其底面用斜二测画法所画出的水平放置的直观图是一个直角边长为的等腰直角三角形(如图所示),则此三棱柱的体积为( ) A. B. C. D. 【答案】D 【解析】由斜二测画法的规则可知,三棱柱的底面为直角三角形,且两条直角边分别为2, ,故此三棱柱的体积为。选D。 7.如图,在正方体中,点是棱上一点,则三棱锥的侧视图是( ) A. B. C. D. 【答案】D 【解析】由题意知三棱锥的侧视图即为三棱锥在侧面上的正投影,点点的投影为,点的投影为,点的投影为,故侧视图为上宽下窄的梯形,且左下到右上的对角线为实线,左上到右下的对角线为虚线,故D选项满足。选D。 点睛:三视图的三种题型 (1)已知几何体画出三视图,解题时要注意画三视图的规则; (2)已知三视图还原几何体,要综合三个视图得到几何体的形状; (3)已知三视图研究几何体,如根据三视图求几何体的体积或表面积等。 8.在正方体中, 和分别为、的中点,那么异面直线与所成角的大小为( ) A. B. C. D. 【答案】C 【解析】试题分析:连接, 为异面直线与所成的角,而为正三角形, 故选C. 【考点】异面直线所成的角. 9.短道速滑队组织6名队员(含赛前系列赛积分最靠前的甲乙丙三名队员在内)进行冬奥会选拔,记“甲得第一名”为,“乙得第二名”为,“丙得第三名”为,若是真命题, 是假命题, 是真命题,则选拔赛的结果为( ) A. 甲得第一名、乙得第二名、丙得第三名 B. 甲得第二名、乙得第一名、丙得第三名 C. 甲得第一名、乙得第三名、丙得第二名 D. 甲得第一名、乙没得第二名、丙得第三名 【答案】D 【解析】由“是真命题”、“是假命题”知,命题一真一假;由“ 是真命题”可得为真命题, 为真命题,故为假命题。综上可得为真命题, 为假命题, 为真命题,从而可得到结论“甲得第一名、乙没得第二名、丙得第三名”。选D。 10.若“”是“”的充分不必要条件,则实数的取值范围是( ) A. B. C. D. 【答案】C 【解析】由解得,因为“”是“”的充分不必要条件,所以Ü,所以,解得,所以实数的取值范围为。选C。 点睛:设对应的集合分别为,则有以下结论: (1)若的充分条件,则; (2)若的充分不必要条件,则Ü ; (3)若的充要条件,则。 根据所给的命题间的充分必要性求参数的取值范围时,要学会根据以上结论将问题转化成集合间的包含关系去处理。 11.如图所示,点是抛物线的焦点,点分别在抛物线及圆的实线部分上运动,且总是平行于轴,则的周长的取值范围( ) A. B. C. D. 【答案】A 【解析】由题意知抛物线的准线为,设两点的坐标分别为, ,则。 由 消去整理得,解得, ∵在图中圆的实线部分上运动, ∴。 ∴的周长为。 选A。 点睛:解决与抛物线有关的问题时,要注意抛物线定义的运用。特别是对于焦点弦的问题更是这样,利用定义可将抛物线上的点到焦点的距离(两点间的距离)转化成该点到准线的距离(点到直线的距离),然后再借助几何图形的性质可使问题的解决变得简单。 12.过双曲线右焦点作一条直线,当直线的斜率为2时,直线与双曲线左右两支各有一个交点;当直线的斜率为3时,直线与双曲线右支有两个不同的交点,则双曲线的离心率的取值范围是 A. B. C. D. 【答案】B 【解析】双曲线的渐近线方程为,由题意得当直线满足条件时应有,又,所以。选B。 二、填空题 13.已知两个球的表面积之比为,则这两个球的半径之比为______. 【答案】 【解析】设两个球的半径分别为,由题意得,解得,即这两个球的半径之比为2:5。 答案:2:5 14.一个几何体的三视图如图所示,则该几何体的表面积为____________ 【答案】 【解析】由题意得该几何体由上下两部分组成,其中上面为圆锥、下面为半球,且圆锥底面圆的半径等于半球的球半径,都为1;圆锥的高为,母线长为。所以几何体的表面积为。答案: 15.已知, 是椭圆和双曲线的公共焦点, 是它们的一个公共点,且,椭圆的离心率为,双曲线的离心率,则_______. 【答案】4 【解析】设椭圆方程为,双曲线方程为, 点为第一象限内的交点,令,则,解得。在中,由余弦定理得 ,即,整理得 ,所以,即。答案:4 点睛:求双曲线离心率的常用方法 (1)根据题意直接求出,由求解; (2)根据条件求得间的关系,由求解; (3)根据条件得到间的二次关系式,然后利用化为关于的二次方程求解。 16.给出以下说法:①不共面的四点中,任意三点不共线; ②有三个不同公共点的两个平面重合; ③没有公共点的两条直线是异面直线; ④分别和两条异面直线都相交的两条直线异面; ⑤一条直线和两条异面直线都相交,则它们可以确定两个平面. 其中正确结论的序号是_______. 【答案】①⑤ 【解析】对于①,若四点中有三点共线时,则必有这四点共面,故①正确。 对于②,当这三个点共线时,则这两个平面不一定重合,故②不正确; 对于③,当两条直线平行时,无公共点,但这两条直线不异面,故③不正确; 对于④,如图,直线为异面直线,直线与两异面直线都相交,但直线有公共点,故④不正确; 对于⑤,当直线和异面直线相交时,则必不共面,所以它们可以确定两个平面,故⑤正确。 综上①⑤正确。答案:①⑤ 点睛:解决点线面位置关系判断题的注意点: (1)正确理解、记忆平面的三个性质及有关的概念; (2)对于有些问题可画出图形,借助图形的直观性进行判断,判断时要注意到对一些特殊情况的处理; (3)要学会运用举反例的方法,以使问题的解决变得方便。 三、解答题 17.如图的三个图中,左面是一个长方体截去一个角所得多面体的直观图,右面是它的正视图和侧视图(单位: ). (1)在正视图下面,按照画三视图的要求画出该多面体的俯视图; (2)按照给出的尺寸,求该多面体的表面积. 【答案】(1)见解析(2) 【解析】(1)俯视图显然是缺一个角的矩形. (2)此几何体是去掉一个小三棱锥的长方体,有长方体的体积减去小三棱锥的体积即可. 18.在极坐标系中,曲线: , : , 与有且仅有一个公共点. (1)求; (2)为极点, , 为上的两点,且,求的最大值. 【答案】(1)(2) 【解析】试题分析:(1)由将曲线、直线极坐标方程化为直角坐标方程, ,再由直线与圆相切得(2)利用极坐标表示: ,再利用三角函数两角差余弦公式及配角公式化为,最后根据正弦函数性质得其最值 试题解析:(1)的直角坐标方程为, 的方程为: ,由已知得. (2)因为为圆,由圆的对称性,设, 则, , 所以当时, 的最大值为. 【考点】极坐标方程化为直角坐标方程,直线与圆位置关系 19.在直角坐标系中,圆的参数方程(为参数).以为极点, 轴的非负半轴为极轴建立极坐标系. (1)求圆的极坐标方程; (2)直线的极坐标方程是,射线: 与圆的交点为、,与直线的交点为,求线段的长. 【答案】(1)(2)2 【解析】试题分析:(1)将参数方程转化为直角坐标系下的普通方程,需要根据参数方程的结构特征,选取恰当的消参方法,常见的消参方法有:代入消参法、加减消参法、平方消参法;(2)将参数方程转化为普通方程时,要注意两种方程的等价性,不要增解、漏解,若有范围限制,要标出的取值范围;(3)掌握,通过圆心距和两圆半径之和、之差的关系判断圆与圆的位置关系;(3)掌握两点间的距离公式. 试题解析:解:(1)圆的普通方程为,得化为极坐标方程为 (2)法一:由;:由 从而 法二:直线,射线 由;:由 从而由两点间距离公式得 【考点】1、极坐标方程;2、直线与圆相交求弦长. 20.已知圆锥曲线:(为参数)和定点,是此圆锥曲线的左、右焦点 (1)以原点为极点,以轴的正半轴为极轴建立极坐标系,求直线的极坐标方程; (2)经过且与直线垂直的直线交此圆锥曲线于两点,求的值. 【答案】(1)(2) 【解析】试题分析:(1)求出椭圆方程的普通方程,求出焦点,运用直线方程的截距式写出直线的直角坐标方程;(2)运用两直线垂直的条件,求得直线的斜率和倾斜角,写出参数方程,代入椭圆方程,由韦达定理及参数的几何意义,即可得到所求. 试题解析:(1)由圆锥曲线(为参数)化为,可得, ∴直线的直角坐标方程为: ,化为. (2)设. ∵直线的斜率为,∴直线的斜率为. ∴直线的方程为:. 代入椭圆的方程可得: ,化为, ,∴. 【考点】(1)椭圆的参数方程;(2)直线与圆锥曲线的关系. 21.设椭圆: 的离心率与双曲线的离心率互为倒数,且椭圆的长轴长为4. (1)求椭圆的标准方程; (2)若直线交椭圆于, 两点, ()为椭圆上一点,求面积的最大值. 【答案】(1)(2) 【解析】试题分析:(Ⅰ)利用椭圆的离心率与双曲线的离心率互为倒数,椭圆的长轴为及,求得的值,进而求得椭圆的方程;(Ⅱ)将直线与(Ⅰ)求得的椭圆方程联立,利用韦达定理和,利用弦长公式及点到直线的距离,求得的面积,同时,进而求得的面积的最大值. 试题解析:(Ⅰ)双曲线的离心率为(1分), 则椭圆的离心率为(2分), 2a=4, (3分) 由⇒,故椭圆M的方程为. (5分) (Ⅱ)由,得, (6分) 由,得﹣2<m<2 ∵,. (7分) ∴=(9分) 又P到AB的距离为. (10分) 则 , (12分) 当且仅当取等号 (13分) ∴. (14分) 【考点】1.椭圆的标准方程;2.韦达定理;3.弦长公式. 22.已知椭圆方程为,双曲线的两条渐近线分别为, ,过椭圆的右焦点作直线,使,又与交于点,设直线与椭圆的两个交点由上至下依次为, . (1)若与所成的锐角为,且双曲线的焦距为4,求椭圆的方程; (2)求的最大值. 【答案】(1)(2)最大值. 【解析】试题分析:(1)首先由题意并结合双曲线的性质可得出, 所满足的关系式,再与 联立求出两者的值即可得出所求的椭圆的方程;(2)首先联立直线与的方程求出它们的交点的坐标,再令,利用引入的参数表示出点的坐标,由于点在椭圆上,代入椭圆的方程结合椭圆的性质求出的取值范围,即可得出所求的最大值. 试题解析: (1)双曲线的渐近线为,两渐近线夹角为60°,又,所以, 所以,所以.又,所以, ,所以椭圆的方程为,所以离心率. (2)由已知, 与联立,解方程组得.设,则,因为,设,则,所以,即,将将A点坐标代入椭圆方程,得, 等式两边同除以, ,所以,当,即时, 有最大值,即的最大值为. 【考点】1、双曲线的简单几何性质;2、双曲线与直线相交的综合问题.查看更多