- 2021-06-15 发布 |
- 37.5 KB |
- 9页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
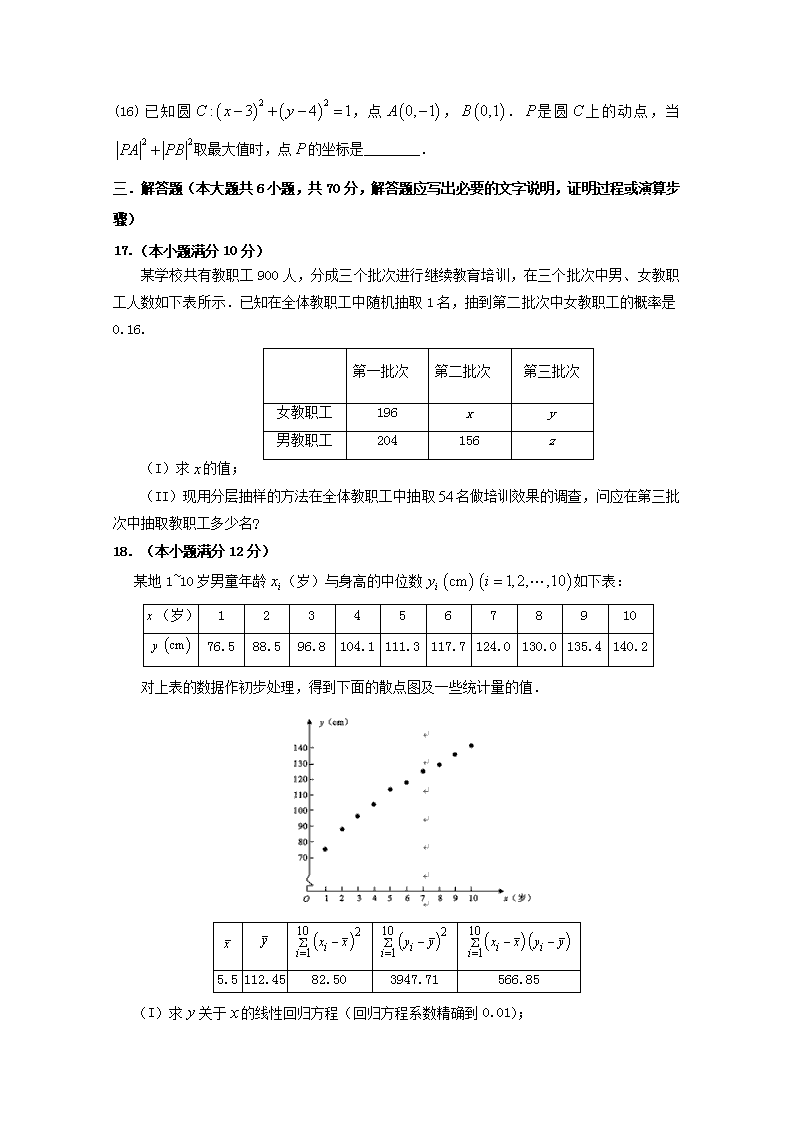
2018-2019学年黑龙江省大庆实验中学高二上学期期中考试数学(理)试题 Word版
大庆实验中学2018-2019学年度上学期期中考试 数学(理)试题 第Ⅰ卷(选择题 共60分) 一.选择题(本题共12小题,每小题5分,共60分,在每小题只有一项是正确的) (1)若与为互斥事件,则( ) (A) (B) (C) (D) (2)条件:动点到两定点距离的和等于定长,条件:动点的轨迹是椭圆,条件是条件的 ( ) (A)充要条件 (B)必要不充分条件 (C)充分不必要条件 (D)既不充分又不必要条件 (3)命题:“若,则”的逆否命题是( ) (A)若,则或 (B)若,则 (C)若或,则 (D)若或,则 (4)在算式大+庆+精+神=中,“大、庆、精、神”分别代表四不同的数字,且依次从大到小,则“庆”字所对应的数字为( ) (A) (B) (C) (D) (5)某个容量为的样本的频率分布直方图如图所示,则在区间上的数据的频数约为( ) (A) (B) (C) (D) 第(6)题 (6)执行如图所示的程序框图,输出的( ) (A) (B) (C) (D) 第(5)题 7)命题“对任意的,”的否定是( ) (A)不存在, (B)存在, (C)存在, (D)对任意的, (8)是一组已知统计数据,其中, 令 , 当( )时,取到最小值 (A) (B) (C) (D) (9)已知是双曲线的两个顶点,为双曲线上(除顶点外) 一点,若直线的斜率乘积为,则双曲线的离心率( ) (A) (B) (C) (D) (10) 抛掷一枚均匀的硬币次,则出现正面的次数多于反面的概率( ) 第(11)题 (A) (B) (C) (D) (11)如图,已知三棱柱的各条棱长都相等,且底面,是侧棱的中点,则异面直线和所成的角为( ) (A) (B) (C) (D) 第(12)题 (12) 如图,若为椭圆上一点,为椭圆的焦点,若以椭圆短轴为直径的圆与相切于中点,则椭圆的方程为( ) (A) (B) (C) (D) 第Ⅱ卷(非选择题 共90分) 二.填空题(本题共4小题,每小题5分,共20分,把正确答案写在答题卡上) (13)从1,2,3,4这四个数中一次随机取两个数,则其中一个数是另一个的两倍的概率为_____. (14)已知、是椭圆的左、右焦点,为椭圆上一点,且.若的面积为,则________. (15)甲乙两人一起去游“西安世园会”,他们约定,各自独立地从1到6号景点中任选4个进行游览,每个景点参观1小时,则最后一小时他们同在一个景点的概率是________. (16)已知圆,点,.是圆上的动点,当取最大值时,点的坐标是________. 三.解答题(本大题共6小题,共70分,解答题应写出必要的文字说明,证明过程或演算步骤) 17.(本小题满分10分) 某学校共有教职工900人,分成三个批次进行继续教育培训,在三个批次中男、女教职工人数如下表所示.已知在全体教职工中随机抽取1名,抽到第二批次中女教职工的概率是0.16. 第一批次 第二批次 第三批次 女教职工 196 x y 男教职工 204 156 z (I)求的值; (II)现用分层抽样的方法在全体教职工中抽取名做培训效果的调查,问应在第三批次中抽取教职工多少名? 18. (本小题满分12分) 某地1~10岁男童年龄(岁)与身高的中位数如下表: (岁) 1 2 3 4 5 6 7 8 9 10 76.5 88.5 96.8 104.1 111.3 117.7 124.0 130.0 135.4 140.2 对上表的数据作初步处理,得到下面的散点图及一些统计量的值. 5.5 112.45 82.50 3947.71 566.85 (I)求关于的线性回归方程(回归方程系数精确到0.01); (II)某同学认为,更适宜作为关于的回归方程类型,他求得的回归方程是.经调查,该地11岁男童身高的中位数为.与(I)中的线性回归方程比较,哪个回归方程的拟合效果更好? 附:回归方程中的斜率和截距的最小二乘估计公式分别为: ,. 19.(本小题满分12分) 求与圆A:外切且与直线l:相切于点的圆B的方程. 20.(本小题满分12分) 某班甲、乙两名同学参加l00米达标训练,在相同条件下两人10次训练的成绩(单位:秒)如下: 1 2 3 4 5 6 7 8 9 10 甲 11.6 12.2 13.2 13.9 14.0 11.5 13.1 14.5 11.7 14.3 乙 12.3 13.3 14.3 11.7 12.0 12.8 13.2 13.8 14.1 12.5 (I)请作出样本数据的茎叶图;如果从甲、乙两名同学中选一名参加学校的100米比赛,从成绩的稳定性方面考虑,选派谁参加比赛更好,并说明理由(不用计算,可通过统计图直接回答结论). (Ⅱ)从甲、乙两人的10次训练成绩中各随机抽取一次,求抽取的成绩中至少有一个比12.8秒差的概率. (Ⅲ)经过对甲、乙两位同学的多次成绩的统计,甲、乙的成绩都均匀分布在之间,现甲、乙比赛一次,求甲、乙成绩之差的绝对值小于秒的概率. 21.(本题满分12分) 如图,已知正方形的边长为,, 将正方形沿对角线折起,得到三棱锥. (I)求证:平面平面; (II)求三棱锥的体积最大时的二面角B-AC-D的余弦值. (Ⅲ)若三棱锥的体积为,求的长. 22.(本小题满分12分) 设点,动圆经过点且和直线相切.记动圆的圆心的轨迹为曲线. (Ⅰ)求曲线的方程; (Ⅱ)过点作互相垂直的直线、分别交曲线于和. 求四边形面积的最小值. 参考答案 一.选择题 DBDBD CCBBC AB 二.填空题 1/3 1/6 三.解答题 17. 解:(1)144 ----------5分 (2)12-----------10分 18. 解:(1)设关于的线性回归方程为 则,, 即----------6分 (2) 当时,用(1)中的方程的 用一元二次回归方程得 由于143.64与145.3更近些,所以用该同学的回归方程拟合效果更好-----12分 19. 解:设所求圆的方程为(x-a)2+(y-b)2=r2(r>0), 由题知所求圆与圆x2+y2-2x=0外切, 则.①-------------------------------2分 又所求圆过点M的切线为直线x+y=0, 故=.②------------------------------------------4分 =r.③------------------------------------------6分 解由①②③组成的方程组得a=4,b=0,r=2或a=0,b=-4,r=6. ------10分 故所求圆的方程为(x-4)2+y2=4或x2+(y+4)2=36.---------------------12分 20.解:(Ⅰ)茎叶图------2分 从统计图中可以看出,乙的成绩较为集中,差异程度较小, 应选派乙同学代表班级参加比赛更好;-------4分 (Ⅱ)设事件A为:甲的成绩低于12.8,事件B为:乙的成绩低于12.8, 则甲、乙两人成绩至少有一个低于秒的概率为: =;--------------8分 (Ⅲ)设甲同学的成绩为,乙同学的成绩为, 则,----------10分 得,如图阴影部分面积即为 ,则 . -------12分 21.(1)证明:因为是正方形, 所以,.-------------------1分 在折叠后的△和△中, 仍有,. 因为,所以平面.--------2分 因为平面, 所以平面平面.------------------3分 (2)二面角的余弦值为(定义法和坐标法同样给分)-------------6分 (3)解:设三棱锥的高为,由于三棱锥的体积为, 所以.因为, 所以.---------8分以下分两种情形求的长: ①当为钝角时,如图,过点作的垂线交的延长线于点,由(1)知平面,所以.又,且,所以平面.所以为三棱锥的高, 即.在△中,因为, 所以.在△中,因为,则. 所以.-------10分 ②当为锐角时,如图,过点作的垂线交于点, 由(1)知平面,所以. 又,且,所以平面. 所以为三棱锥的高,即.在△中,因为, 所以 在△中,因为,则. 所以. 综上可知,的长为或.-----------12分 22.解(Ⅰ)过点作垂直直线于点 依题意得. ---------2分 所以动点的轨迹为是以为焦点,直线为准线的抛物线.--4分 即曲线的方程是 ------------6分 (Ⅱ)依题意,直线的斜率存在且不为, 设直线的方程为,由得的方程为. 将代入 化简得. -------------8分 设 则 同理可得 ---------------10分 四边形的面积 当且仅当 即时, 故四边形面积的最小值是 ----------12分查看更多