- 2021-06-15 发布 |
- 37.5 KB |
- 6页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高三数学二轮高考专题辅导与训练打包检测试题:专题一第2讲课时训练提能
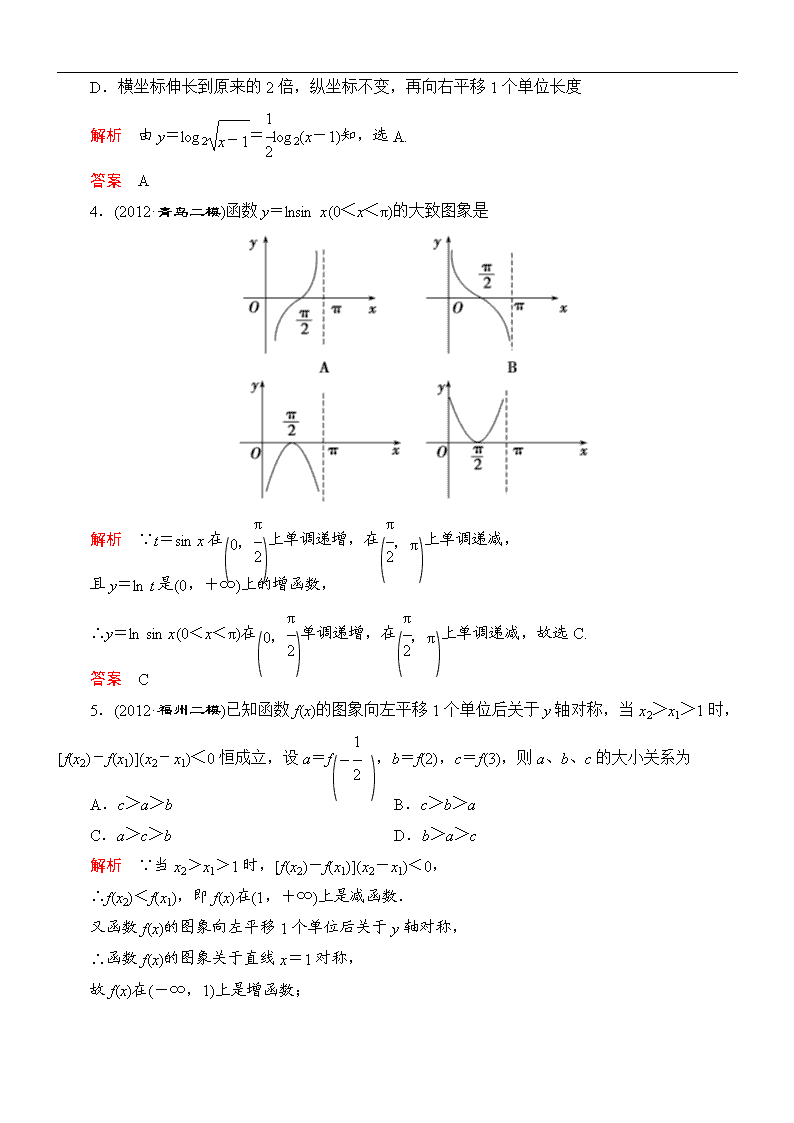
专题一 第2讲 函数的图象与性质 课时训练提能 [限时45分钟,满分75分] 一、选择题(每小题4分,共24分) 1.函数f(x)=+lg(2x-1)的定义域是 A.(-∞,1) B.(0,1] C.(0,1) D.(0,+∞) 解析 要使函数有意义,自变量x必须满足得解得0<x<1, 即函数的定义域为(0,1). 答案 C 2.(2012·天津二模)已知f(x)=则f+f的值为 A. B.- C.-1 D.1 解析 f=cos=cos π=-. f=f+1=f+1=+1=f+2=cos+2=-+2=, ∴f+f=1. 答案 D 3.(2012·武汉模拟)为了得到函数y=log2的图象,可将函数y=log2x的图象上所有的点的 A.纵坐标缩短到原来的倍,横坐标不变,再向右平移1个单位长度 B.纵坐标缩短到原来的倍,横坐标不变,再向左平移1个单位长度 C.横坐标伸长到原来的2倍,纵坐标不变,再向左平移1个单位长度 D.横坐标伸长到原来的2倍,纵坐标不变,再向右平移1个单位长度 解析 由y=log2=log2(x-1)知,选A. 答案 A 4.(2012·青岛二模)函数y=lnsin x(0<x<π)的大致图象是 解析 ∵t=sin x在上单调递增,在上单调递减, 且y=ln t是(0,+∞)上的增函数, ∴y=ln sin x(0<x<π)在单调递增,在上单调递减,故选C. 答案 C 5.(2012·福州二模)已知函数f(x)的图象向左平移1个单位后关于y轴对称,当x2>x1>1时,[f(x2)-f(x1)](x2-x1)<0恒成立,设a=f,b=f(2),c=f(3),则a、b、c的大小关系为 A.c>a>b B.c>b>a C.a>c>b D.b>a>c 解析 ∵当x2>x1>1时,[f(x2)-f(x1)](x2-x1)<0, ∴f(x2)<f(x1),即f(x)在(1,+∞)上是减函数. 又函数f(x)的图象向左平移1个单位后关于y轴对称, ∴函数f(x)的图象关于直线x=1对称, 故f(x)在(-∞,1)上是增函数; 由于|3-1|>>|2-1|,∴f(3)<f<f(2),即c<a<b. 答案 D 6.设函数y=f(x)在(-∞,+∞)内有定义,对于给定的正数K,定义函数:fK(x)=取函数f(x)=a-|x|(a>1),当K=时,函数fK(x)在下列区间上单调递减的是 A.(-∞,0) B.(-a,+∞) C.(-∞,-1) D.(1,+∞) 解析 如图所示,先作出函数f(x)=a-|x|(a>1)的图象,然后作出直线y=,则函数fK(x)的图象为图中实线部分,显然函数fK(x)=故函数fK(x)在(-∞,-1)上单调递增,在[-1,1]上为常数,在(1,+∞)上单调递减.故选D. 答案 D 二、填空题(每小题5分,共15分) 7.(2012·邯郸模拟)已知f(x)=则不等式x+x·f(x)≤2的解集是________. 解析 原不等式等价于或解得0≤x≤1或x<0. ∴原不等式的解集为(-∞,1]. 答案 (-∞,1] 8.函数f(x)的定义域为R,f(-1)=2,对任意x∈R,f′(x)>2,则f(x)>2x+4的解集为________. 解析 令函数g(x)=f(x)-2x-4,则g′(x)=f′(x)-2>0, 因此g(x)在R上是增函数, 又因为g(-1)=f(-1)+2-4=2+2-4=0, 所以原不等式可化为:g(x)>g(-1), 由g(x)的单调性可得x>-1, 所以原不等式的解集为(-1,+∞). 答案 (-1,+∞) 9.(2012·惠州二模)四位同学在研究函数f(x)=(x∈R)时,分别给出下面四个结论: ①函数f(x)的值域为(-1,1); ②若x1≠x2,则一定有f(x1)≠f(x2); ③f(x)是连续且递增的函数,但f′(0)不存在; ④若规定f1(x)=f(x),fn+1(x)=f[fn(x)],则fn(x)=对任意n∈N+恒成立. 上述四个结论中正确的有________. 解析 当x>0时,f(x)==1-. ∵x>0,∴f(x)∈(0,1). ∵f(x)是奇函数,∴当x<0时,f(x)∈(-1,0), 又f(0)=0,故f(x)∈(-1,1),故①正确; 当x>0时,f(x)==1-, ∴f′(x)=>0, 即f(x)在(0,+∞)上单调递增. 又∵f(x)是奇函数,且f(0)=0, ∴f(x)在(-∞,+∞)上是单调递增函数,故②正确;③错误. 当x>0时,f(x)=>0, ∴fn+1(x)=,=+1, ∴=+1×(n-1)=+n-1=, ∴fn(x)=,同理,当x<0时,fn(x)=, 故对任意n∈N+,都有fn(x)=,故④正确. 答案 ①②④ 三、解答题(每小题12分,共36分) 10.(1)已知定义域为R的函数f(x)满足f[f(x)-x2+x]=f(x)-x2+x,若f(3)=1,求f(-5); (2)设f(2cos x-1)=sin2x,求f. 解析 (1)在f[f(x)-x2+x]=f(x)-x2+x中,令x=3,得f[f(3)-32+3]=f(3)-32+3, ∵f(3)=1,∴f(1-32+3)=1-32+3, 即f(-5)=-5. (2)解法一 令2cos x-1=,解得cos x=, 故sin2x=1-cos2x =1-2=. 故f=. 解法二 令2cos x-1=t,解得cos x=, 又cos x∈[-1,1],所以t∈[-3,1]. 而sin2x=1-cos2x=1-2=, ∴f(t)=,故f(x)=(x∈[-3,1]). ∴f==. 11.已知f(x)是R上的奇函数,且f(x+2)=-f(x).当-1≤x≤1,f(x)=x3. (1)求证:x=1是函数y=f(x)的一条对称轴; (2)当x∈(1,5)时,求f(x)的表达式. 解析 (1)证明 因为f(x)为奇函数,所以-f(x)=f(-x). 因为f(x+2)=f(-x),所以f[(x-1)+2]=f[-(x-1)]. 即f(1+x)=f(1-x), 所以直线x=1是函数f(x)图象的一条对称轴. (2)因为f(x+4)=-f(x+2)=f(x), 所以f(x)是以4为周期的函数. 又-1≤x≤1时,f(x)=x3, 当x∈[1,3]时,x-2∈[-1,1], 所以f(x)=f(x-2+2)=-f(x-2)=-(x-2)3. 当x∈(3,5]时,x-4∈(-1,1], 所以f(x)=f(x-4+4)=f(x-4)=(x-4)3. 所以当x∈[1,5]时,f(x)的解析式为f(x)= 12.(2012·大连模拟)若定义在R上的函数f(x)对任意x1,x2∈R,都有f(x1+x2)=f(x1)+f(x2)-1成立,且当x>0时,f(x)>1. (1)求证:f(x)-1为奇函数; (2)求证:f(x)是R上的增函数; (3)若f(4)=5,解不等式f(3m2-m-2)<3. 解析 (1)证明 ∵定义在R上的函数f(x)对任意x1,x2∈R,都有f(x1+x2)=f(x1)+f(x2)-1成立. 令x1=x2=0,则f(0+0)=f(0)+f(0)-1,即f(0)=1. 令x1=x,x2=-x, f(x-x)=f(x)+f(-x)-1, ∴[f(x)-1]+[f(-x)-1]=0, ∴f(x)-1为奇函数. (2)证明 ∵由(1),知f(x)-1为奇函数, ∴f(x)-1=-[f(-x)-1]. 任取x1,x2∈R,且x1<x2,则x2-x1>0, ∵f(x1+x2)=f(x1)+f(x2)-1, ∴f(x2-x1)=f(x2)+f(-x1)-1 =f(x2)-[f(x1)-1]=f(x2)-f(x1)+1, ∵当x>0时,f(x)>1, ∴f(x2-x1)=f(x2)-f(x1)+1>1, ∴f(x1)<f(x2), ∴f(x)是R上的增函数. (3)∵f(x1+x2)=f(x1)+f(x2)-1,且f(4)=5, ∴f(4)=f(2)+f(2)-1=5,即f(2)=3, 由不等式f(3m2-m-2)<3, 得f(3m2-m-2)<f(2). 由(2),知f(x)是R上的增函数, ∴3m2-m-2<2,即3m2-m-4<0,则-1<m<, ∴不等式f(3m2-m-2)<3的解集为.查看更多