2018届二轮复习　解析几何中的范围、定值和探索性问题学案（全国通用）

2018届二轮复习　解析几何中的范围、定值和探索性问题学案（全国通用）

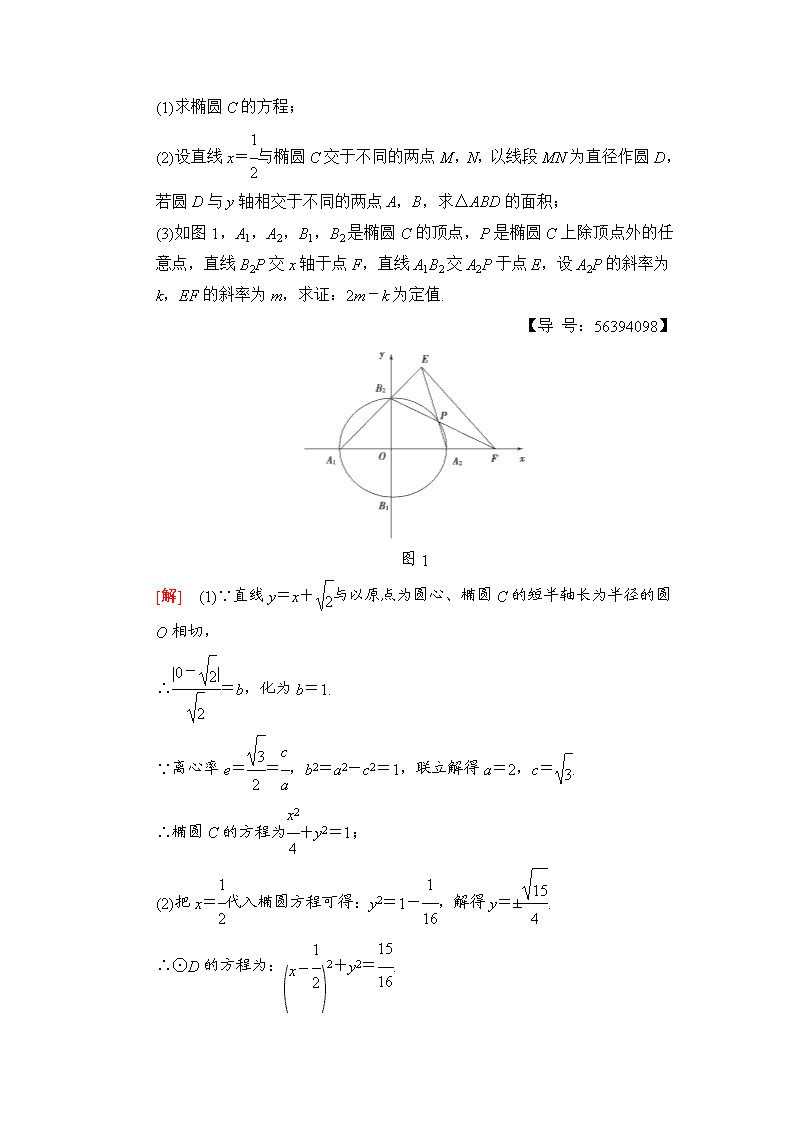
难点四　‎ 解析几何中的范围、定值和探索性问题 ‎(对应 生用书第68页)‎ 解析几何中的范围、定值和探索性问题仍是高考考试的重点与难点，主要以解答题形式考查，一般以椭圆为背景，考查范围、定值和探索性问题，试题难度较大．复习时不能把目标仅仅定位在知识的掌握上，要在解题方法、解题思想上深入下去．解析几何中基本的解题方法是使用代数方程的方法研究直线、曲线的某些几何性质，代数方程是解题的桥梁，要掌握一些解方程(组)的方法，掌握一元二次方程的知识在解析几何中的应用，掌握使用根与系数的关系进行整体代入的解题方法；其次注意分类讨论思想、函数与方程思想、化归与转化思想等的应用，如解析几何中的最值问题往往需建立求解目标函数，通过函数的最值研究几何中的最值．下面对这些难点一一分析：‎ ‎1．圆锥曲线中的定点、定值问题 该类问题多以直线与圆锥曲线为背景，常与函数与方程、向量等知识交汇，形成了过定点、定值等问题的证明，难度较大．定点、定值问题是在变化中所表现出 的不变的量，那么就可以用变化的量表示问题的直线方程、数量积、比例关系等，这些直线方程、数量积、比例关系不受变化的量所影响的一个点、一个值，就是要求的定点、定值．化解这类问题的关键就是引进变的参数表示直线方程、数量积、比例关系等，根据等式的恒成立、数式变换等寻找不受参数影响的量．‎ ‎【例1】　(2017·江苏省南京市迎一模模拟)设椭圆C：＋＝1(a＞b＞0)的离心率e＝，直线y＝x＋与以原点为圆心、椭圆C的短半轴长为半径的圆O相切．‎ ‎(1)求椭圆C的方程；‎ ‎(2)设直线x＝与椭圆C交于不同的两点M，N，以线段MN为直径作圆D，若圆D与y轴相交于不同的两点A，B，求△ABD的面积；‎ ‎(3)如图1，A1，A2，B1，B2是椭圆C的顶点，P是椭圆C上除顶点外的任意点，直线B2P交x轴于点F，直线A1B2交A2P于点E，设A2P的斜率为k，EF的斜率为m，求证：‎2m－k为定值. ‎ ‎【导 号：56394098】‎ 图1‎ ‎[解]　(1)∵直线y＝x＋与以原点为圆心、椭圆C的短半轴长为半径的圆O相切，‎ ‎∴＝b，化为b＝1.‎ ‎∵离心率e＝＝，b2＝a2－c2＝1，联立解得a＝2，c＝.‎ ‎∴椭圆C的方程为＋y2＝1；‎ ‎(2)把x＝代入椭圆方程可得：y2＝1－，解得y＝±.‎ ‎∴⊙D的方程为：2＋y2＝.‎ 令x＝0，解得y＝±，‎ ‎∴|AB|＝，∴S△ABD＝|AB|·|OD|＝××＝.‎ ‎(3)证明：由(1)知：A1(－2,0)，A2(2,0)，B2(0,1)，‎ ‎∴直线A1B2的方程为y＝x＋1，‎ 由题意，直线A2P的方程为y＝k(x－2)，k≠0，且k≠±，‎ 由解得E.‎ 设P(x1，y1)，则由得(4k2＋1)x2－16k2x＋16k2－4＝0.‎ ‎∴2x1＝，∴x1＝，y1＝k(x1－2)＝.‎ ‎∴P.‎ 设F(x2,0)，则由P，B2，F三点共线得，kB2P＝kB‎2F.‎ 即＝，∴x2＝，∴F.‎ ‎∴EF的斜率m＝＝.‎ ‎∴‎2m－k＝－k＝为定值．‎ ‎[方法总结]　定值问题是解析几何中的一种常见问题，基本的求解思想是：先用变量表示所需证明的不变量，然后通过推导和已知条件，消去变量，得到定值，即解决定值问题首先是求解非定值问题，即变量问题，最后才是定值问题．‎ ‎(1)求定值问题常见的方法有两种 ‎①从特殊入手，求出定值，再证明这个值与变量无关．‎ ‎②直接推理、计算，并在计算推理的过程中消去变量，从而得到定值．‎ ‎(2)定点的探索与证明问题 ‎①探索直线过定点时，可设出直线方程为y＝kx＋m，然后利用条件建立k，m等量关系进行消元，借助于直线系的思想找出定点．‎ ‎②从特殊情况入手，先探求定点，再证明与变量无关．‎ ‎2．圆锥曲线中的最值、范围问题 圆锥曲线中参数的范围及最值问题，由于其能很好地考查 生对数 知识的迁移、组合、融会的能力，有利于提高 生综合运用所 知识分析、解决问题的能力．该类试题设计巧妙、命题新颖别致，常求特定量、 特定式子的最值或范围．常与函数解析式的求法、函数最值、不等式等知识交汇，成为近年高考热点．解决圆锥曲线中最值、范围问题的基本思想是建立目标函数和建立不等关系，根据目标函数和不等式求最值、范围，因此这类问题的难点，就是如何建立目标函数和不等关系．建立目标函数或不等关系的关键是选用一个合适变量，其原则是这个变 量能够表达要解决的问题，这个变量可以是直线的斜率、直线的截距、点的坐标等，要根据问题的实际情况灵活处理．‎ 图2‎ ‎【例2】　(苏北四市(徐州、淮安、连云港、宿迁)2017届高三上 期期末)如图2，在平面直角坐标系xOy中，已知椭圆C：＋＝1(a＞b＞0)的离心率为，且右焦点F到左准线的距离为6.‎ ‎(1)求椭圆C的标准方程；‎ ‎(2)设A为椭圆C的左顶点，P为椭圆C上位于x轴上方的点，直线PA交y轴于点M，过点F作MF的垂线，交y轴于点N.‎ ‎(ⅰ)当直线的PA斜率为时，求△FMN的外接圆的方程；‎ ‎(ⅱ)设直线AN交椭圆C于另一点Q，求△APQ的面积的最大值．‎ ‎[解]　(1)由题意，得解得 则b＝2，‎ 所以椭圆C的标准方程为＋＝1.‎ ‎(2)由题可设直线PA的方程为y＝k(x＋4)，k＞0，则M(0,4k)，‎ 所以直线FN的方程为y＝(x－2)，则N .‎ ‎(ⅰ)当直线PA的斜率为，即k＝时，M(0,2)，N(0，－4)，F(2，0)，＝(2，－2)，＝(－2，－4)，·＝－8＋8＝0.‎ 所以MF⊥FN，所以圆心为(0，－1)，半径为3，‎ 所以△FMN的外接圆的方程为x2＋(y＋1)2＝9.‎ ‎(ⅱ)联立消去y并整理得，(1＋2k2)x2＋16k2x＋32k2－16＝0，‎ 解得x1＝－4或x2＝，所以P，‎ 直线AN的方程为y＝－(x＋4)，同理可得，Q，‎ 所以P，Q关于原点对称，即PQ过原点．‎ 所以△APQ的面积S＝OA·(yP－yQ)＝2×＝≤8，当且仅当2k＝，即k＝时，取“＝”．‎ 所以△APQ的面积的最大值为8.‎ ‎[方法总结]　这类问题在题目中往往没有给出不等关系，需要我们去寻找．求最值或范围常见的解法：(1)几何法：若题目的条件和结论能明显体现几何特征及意义，可考虑利用图形性质 解决；(2)代数法：若题目的条件和结论能体现一种明确的函数关系，则可首先建立目标函数，再求最值，求函数最值常用的方法有配方法、判别式法、导数法、基本不等式法及函数的单调性、有界性法等．用这种方法求解圆锥曲线的最值与范围问题时，除了重视建立函数关系式这个关键点外，还要密切注意所建立的函数式中的变量是否有限制范围，这些限制范围恰好制约了最值的取得，因此在解题时要予以高度关注．‎ ‎3．圆锥曲线中的探索性问题 探索性问题主要考查 ‎ 生探索解题途径，解决非传统完备问题的能力，是命题者根据 特点，将数 知识有机结合并赋予新的情境创设而成的，要求 生自己观察、分析、创造性地运用所 知识和方法解决问题，它能很好地考查数 思维能力以及 的探索精神．因此越 越受到高考命题者的青睐．探索性问题实质上是探索结论的开放性问题．相对于其他的开放性问题 说，由于这类问题的结论较少(只有存在、 不存在两个结论有时候需讨论)，因此，思考途径较为单一，难度易于控制，受到各类考试命题者的青睐．解答这一类问题，往往从承认结论、变结论为条件出发，然后通过特例归纳，或由演绎推理证明其合理性．探索过程要充分挖掘已知条件，注意条件的完备性，不要忽略任何可能的因素．‎ 图3‎ ‎【例3】　(苏北四市(淮安、宿迁、连云港、徐州)2017届高三上 期期中)如图3，在平面直角坐标系xOy中，已知圆C：x2＋y2－4x＝0及点A(－1,0)，B(1,2)．‎ ‎(1)若直线l平行于AB，与圆C相交于M，N两点，MN＝AB，求直线l的方程；‎ ‎(2)在圆C上是否存在点P满足条件，使得PA2＋PB2＝12？若存在，求点P的个数；若不存在，说明理由．‎ ‎ 【导 号：56394099】‎ ‎[解]　(1)圆C的标准方程为(x－2)2＋y2＝4，所以圆心C(2,0)，半径为2.‎ 因为l∥AB，A(－1,0)，B(1,2)，所以直线l的斜率为＝1，‎ 设直线l的方程为x－y＋m＝0，‎ 则圆心C到直线l的距离为d＝＝.‎ 因为MN＝AB＝＝2，‎ 而CM2＝d2＋2，所以4＝＋2，‎ 解得m＝0或m＝－4，‎ 故直线l的方程为x－y＝0或x－y－4＝0.‎ ‎(2)假设圆C上存在点P满足条件，设P(x，y)，则(x－2)2＋y2＝4，‎ PA2＋PB2＝(x＋1)2＋(y－0)2＋(x－1)2＋(y－2)2＝12，‎ 即x2＋y2－2y－3＝0，即x2＋(y－1)2＝4，‎ 因为|2－2|＜＜2＋2，‎ 所以圆(x－2)2＋y2＝4与圆x2＋(y－1)2＝4相交，‎ 所以点P的个数为2.‎ ‎[方法总结]　(1)解决存在性问题的解题步骤：第一步：先假设存在，引入参变量，根据题目条件列出关于参变量的方程(组)或不等式(组)；第二步：解此方程(组)或不等式(组)，若有解则存在，若无解则不存在；第三步：得出结论．(2)解决存在性问题应注意以下几点：①当条件和结论不唯一时要分类讨论；②当给出结论而要推导出存在的条件时，先假设成立，再推出条件；③当条件和结论都不知，按常规方法解题很难时，要思维开放，采取另外的途径．‎