2017-2018学年安徽省蚌埠市第二中学高二下学期期中考试数学(文)试题 Word版
蚌埠二中2017-2018学年第二学期期中考试
高二数学(文)试题
试卷满分:150分;考试时间:120分钟
第I卷(选择题)
一.选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项符合题目要求的.
1. 已知集合,则中元素的个数为( )
A.必有1个 B.1个或2个 C.至多1个 D.可能2个以上
2.在复平面内,复数对应的点的坐标为,则在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3下列有关命题的说法错误的是( )
A. 若“”为假命题,则均为假命题
B. “”是“”的充分不必要条件
C. “”的必要不充分条件是“”
D. 若命题p:,则命题:
4某家庭连续五年收入x与支出y如表:
年份
2013
2014
2015
2016
2017
收入万元
支出万元
画散点图知:y与x线性相关,且求得的回归方程是,其中,则据此预计该家庭2018年若收入15万元,支出为( )万元.
A. B. C. D.
5.已知{bn}为等比数列,b5=2,则b1b2b3…b9=29.若{an}为等差数列,
a5=2,则{an}的类似结论为( )
A.a1a2a3…a9=29 B.a1+a2+…+a9=29
C.a1a2…a9=2×9 D.a1+a2+…+a9=2×9
6已知函数在R上可导,其部分图象如图所示,设,
则下列不等式正确的是
A. B.
B. C. D.
7. 宋元时期数学著名《算学启蒙》中有关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.如图是源于其思想的一个程序框图,若输入的、分别为5、2,则输出的( )
A. 2 B. 3 C. 4 D. 5
8.已知椭圆+=1(m>0)与双曲线=1(n>0)有相同的焦点,则m+n的最大值是( )
A.3 B.6 C.18 D.36
9.血药浓度(Plasma
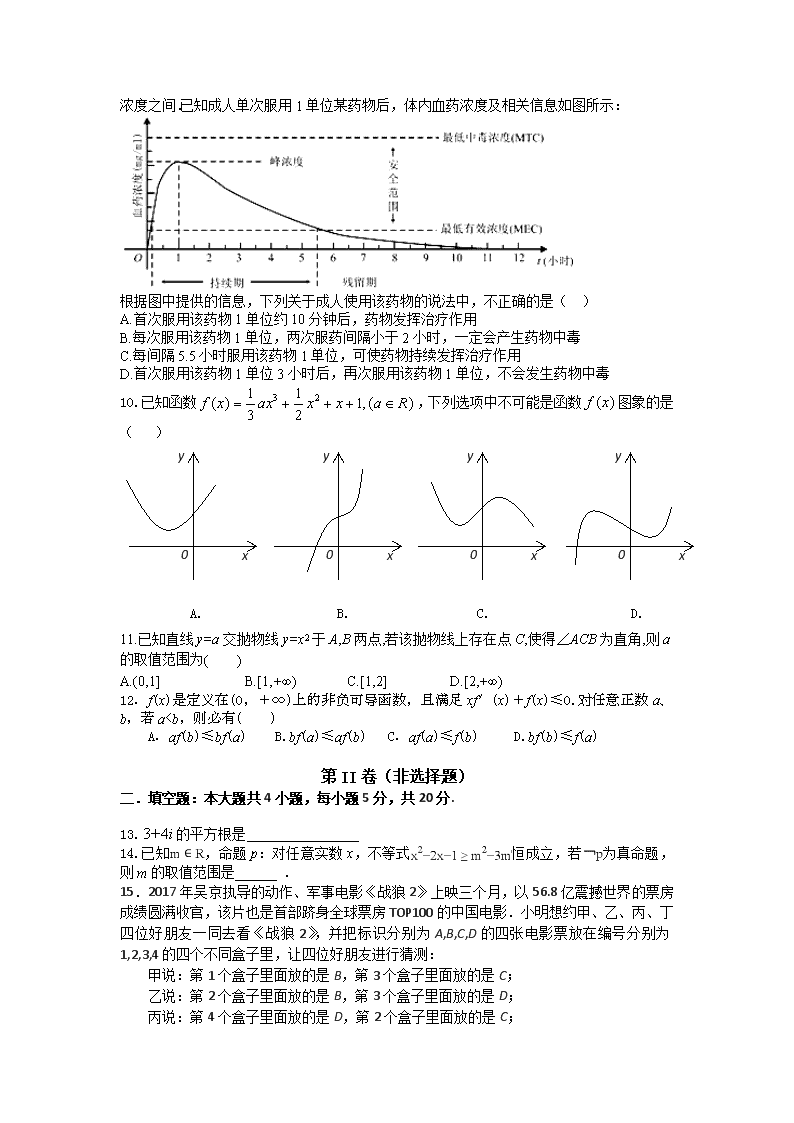
Concentration)是指药物吸收后在血浆内的总浓度.药物在人体内发挥治疗作用时,该药物的血药浓度应介于最低有效浓度和最低中毒浓度之间.已知成人单次服用1单位某药物后,体内血药浓度及相关信息如图所示:
根据图中提供的信息,下列关于成人使用该药物的说法中,不正确的是( )
A.首次服用该药物1单位约10分钟后,药物发挥治疗作用
B.每次服用该药物1单位,两次服药间隔小于2小时,一定会产生药物中毒
C.每间隔5.5小时服用该药物1单位,可使药物持续发挥治疗作用
D.首次服用该药物1单位3小时后,再次服用该药物1单位,不会发生药物中毒
10.已知函数,下列选项中不可能是函数图象的是( )
0
x
y
0
x
y
0
x
y
0
x
y
A. B. C. D.
11.已知直线y=a交抛物线y=x2于A,B两点,若该抛物线上存在点C,使得∠ACB为直角,则a的取值范围为( )
A.(0,1] B.[1,+∞) C.[1,2] D.[2,+∞)
12.f(x)是定义在(0,+∞)上的非负可导函数,且满足xf′(x)+f(x)≤0.对任意正数a、b,若a
0,b>0)的右顶点为A,以A为圆心,b为半径作圆A,圆A与双曲线C的一条渐近线交于M、N两点.若∠MAN=60°,则C的离心率为________.
三、解答题:解答应写出文字说明、证明过程或演算步骤。
17.(本小题10分)已知,,其中.
(1)若且为真,求的取值范围;
(2)若是的充分不必要条件,求实数的取值范围.
18. (本小题12分)环境问题是当今世界共同关注的问题,我国环保总局根据空气污染指数浓度,制定了空气质量标准:
空气污染指数
空气质量等级
优
良
轻度污染
中度污染
重度污染
严重污染
某市政府为了打造美丽城市,节能减排,从2010年开始考察了连续六年11月份的空气污染指数,绘制了频率分布直方图,经过分析研究,决定从2016年11月1日起在空气质量重度污染和严重污染的日子对机动车辆限号出行,即车牌尾号为单号的车辆单号出行,车牌尾号为双号的车辆双号出行(尾号是字母的,前13个视为单号,后13个视为双号),王先生有一辆车,若11月份被限行的概率为0.05.
(1)求频率分布直方图中的值(写出推理过程,直接写出答案不得分);
(2)若按分层抽样的方法,从空气质量良好与中度污染的天气中抽取6天,再从这6天中随机抽取2天,求至少有一天空气质量中度污染的概率;
(3)该市环保局为了调查汽车尾气排放对空气质量的影响,对限行两年来的11月份共60天的空气质量进行统计,其结果如下表:
根据限行前6年180天与限行后60天的数据,计算并填写以下列联表,并回答是否有的把握认为空气质量的优良与汽车尾气的排放有关.
参考数据:
参考公式:,其中.
19. (本小题12分)已知不等式的解集为.
(Ⅰ)求的值;
(Ⅱ)若, , ,求证: .
20.(本小题12分)在直角坐标系xOy中,曲线C1的参数方程为(φ为参数),以原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=4sinθ
(Ⅰ)求曲线C1的普通方程和C2的直角坐标方程;
(Ⅱ)已知曲线C3的极坐标方程为θ=α,0<α<π,ρ∈R,点A是曲线C3与C1的交点,点B是曲线C3与C2的交点,且A,B均异于原点O,且|AB|=4,求实数α的值.
21. (本小题12分)已知椭圆:的左、右焦点分别是、,离心率,过点的直线交椭圆于、两点,的周长为16.
(1)求椭圆的方程;
(2)已知为原点,圆:()与椭圆交于、两点,点为椭圆上一动点,若直线、与轴分别交于、两点,求证:为定值.
22.(本小题12分)已知函数,.
(1)当时,求函数在点处的切线方程;
(2)当时,令函数,若函数在区间上有两个零点,求实数的取值范围.
蚌埠二中2017-2018学年第二学期期中考试
高二数学(文)答案
一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1
2
3
4
5
6
7
8
9
10
11
12
C
D
C
B
D
B
C
B
D
D
B
A
二、 填空题:本大题共4小题,每小题5分。
13 14 .
15 D或 A 16
三、解答题:解答应写出文字说明、证明过程或演算步骤。(17题10分,18-22题每题12分)
17.解:(1)由,解得,所以
又,因为,解得,所以.
当时,,又为真,都为真,所以.
18.解:(1)因为限行分单双号,王先生的车被限行的概率为0.05,
所以空气重度污染和严重污染的概率应为,
由频率分布直方图可知:,
∴.
(2)因为空气质量良好与中度污染的天气的概率之比为,
按分层抽样从中抽取6天,则空气质量良好天气被抽取4天,记做,
空气中度污染天气被抽取2天,记做,
再从这6天中随机抽取2天,所包含的基本事件有:共15个,
事件“至少有一天空气质量中度污染”所包含的基本事件有:共9个,
故.
(3)列联表如下:
因为,
所以至少有的把握认为空气质量的优良与汽车尾气的排放有关.
19.(Ⅰ)由,
得或或,
解得,∴, .
(Ⅱ)由(Ⅰ)知, , ,
∴ ,
当且仅当即, 时取等号,
∴,即.
20.解:(Ⅰ)由曲线C1的参数方程为(φ为参数),
消去参数得曲线C1的普通方程为(x﹣2)2+y2=4.
∵曲线C2的极坐标方程为ρ=4sinθ,∴ρ2=4ρsinθ,
∴C2的直角坐标方程为x2+y2=4y,整理,得x2+(y﹣2)2=4.
(Ⅱ)曲线C1:(x﹣2)2+y2=4化为极坐标方程为ρ=4cosθ,
设A(ρ1,α1),B(ρ2,α2),
∵曲线C3的极坐标方程为θ=α,0<α<π,ρ∈R,点A是曲线C3与C1的交点,
点B是曲线C3与C2的交点,且A,B均异于原点O,且|AB|=4,
∴|AB|=|ρ1﹣ρ2|=|4sinα﹣4cosα|=4|sin()|=4,
∴sin()=±1,
∵0<α<π,∴∴,解得
21.【解析】(1)由题意得,则,·······2分
由,解得,·······4分
则,所以椭圆的方程为.·······6分
(2)证明:由条件可知,,两点关于轴对称,设,,则,由题可知,,,
∴,.·······8分
又直线的方程为,
令得点的横坐标,·······10分
同理可得点的横坐标.
∴,即为定值.·······12分
22.【解析】(1)当时,.
当时,,所以点为,···········1分
又,因此.···········2分
因此所求切线方程为.···········4分
(2)当时,,
则.···········6分
因为,所以当时,,···········7分
且当时,;当时,;
故在处取得极大值也即最大值.···········8分
又,,
,
则,所以在区间上的最小值为,······10分
故在区间上有两个零点的条件是,
所以实数的取值范围是.···········12分