2020年高考数学(理)二轮复习讲练测 专题22 几何体的表面积与体积的求解（练）（原卷版）

2020年高考数学(理)二轮复习讲练测 专题22 几何体的表面积与体积的求解（练）（原卷版）

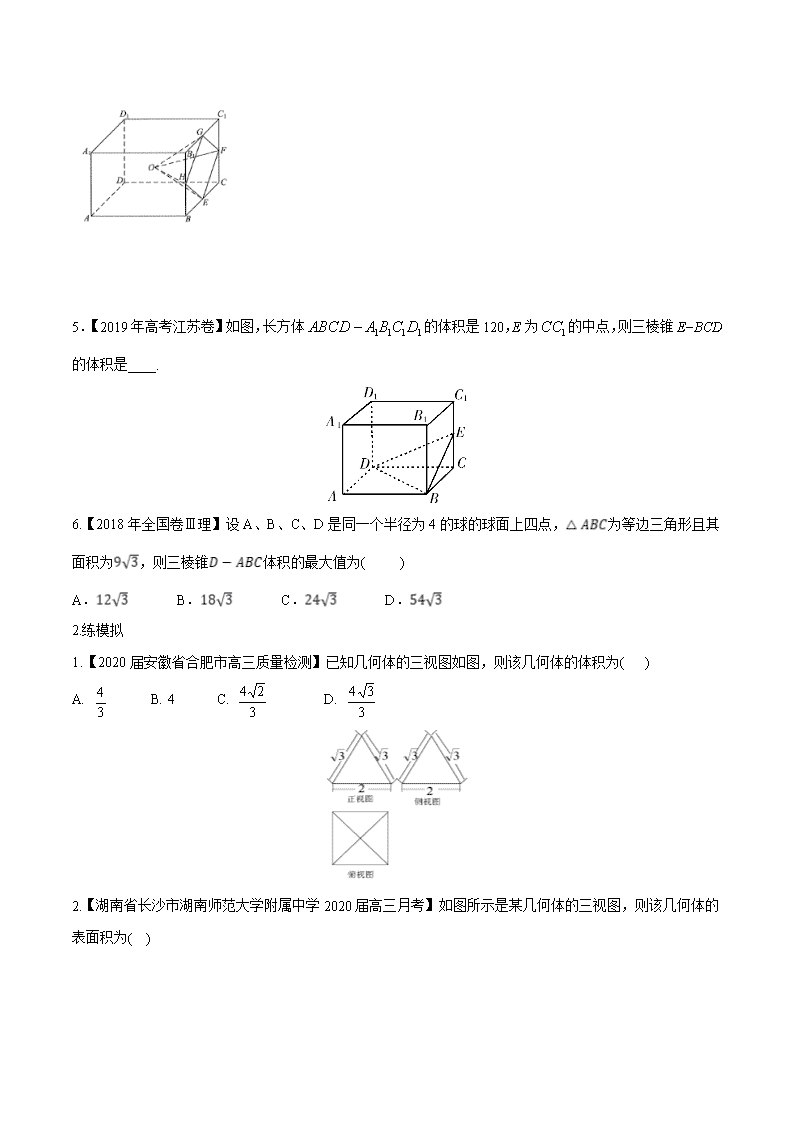
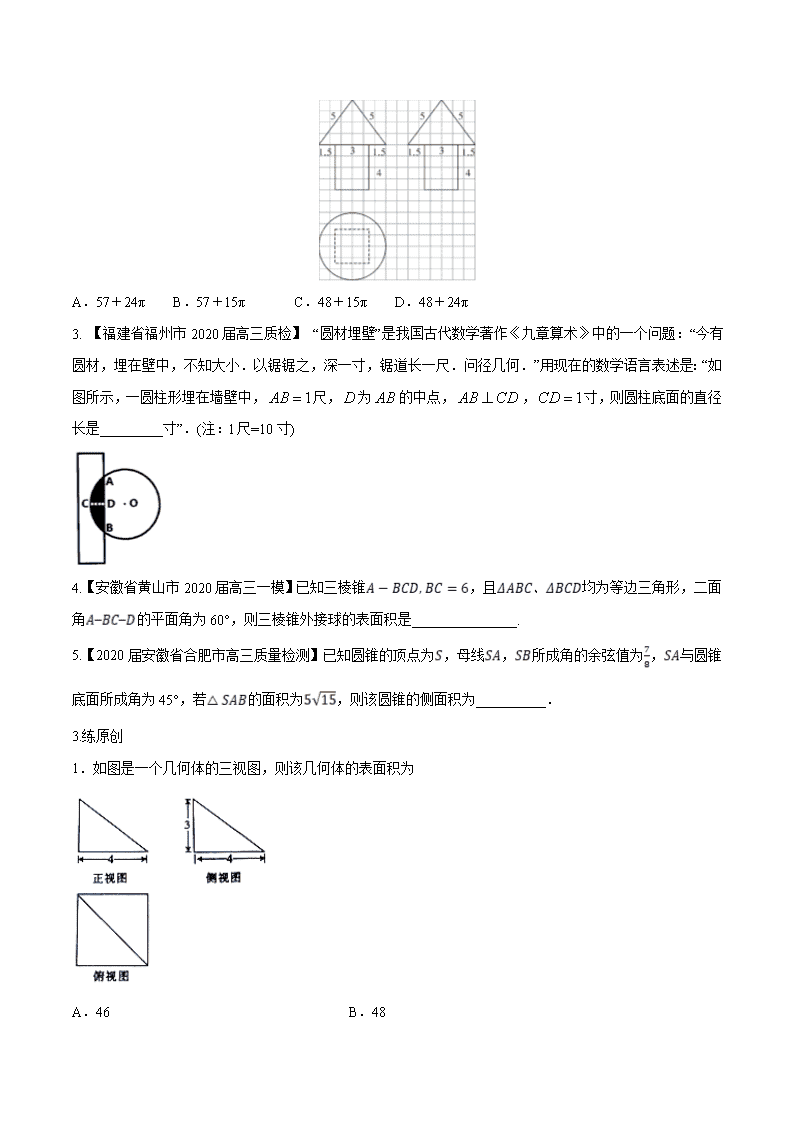
专题22 几何体的表面积与体积的求解 ‎1、【2019年高考全国Ⅰ卷理数】已知三棱锥P−ABC的四个顶点在球O的球面上，PA=PB=PC，△ABC是边长为2的正三角形，E，F分别是PA，AB的中点，∠CEF=90°，则球O的体积为 A． B．‎ C． D．‎ ‎2．【2019年高考浙江卷】祖暅是我国南北朝时代的伟大科学家，他提出的“幂势既同，则积不容异”称为祖暅原理，利用该原理可以得到柱体的体积公式V柱体=Sh，其中S是柱体的底面积，h是柱体的高．若某柱体的三视图如图所示(单位：cm)，则该柱体的体积(单位：cm3)是 A．158 B．162 ‎ C．182 D．324‎ ‎3．【2019年高考天津卷理数】已知四棱锥的底面是边长为的正方形，侧棱长均为．若圆柱的一个 底面的圆周经过四棱锥四条侧棱的中点，另一个底面的圆心为四棱锥底面的中心，则该圆柱的体积为 _．‎ ‎4．【2019年高考全国Ⅲ卷理数】学生到工厂劳动实践，利用3D打印技术制作模型.如图，该模型为长方体 挖去四棱锥O—EFGH后所得的几何体，其中O为长方体的中心，E，F，G，H分别为所在棱的中点，，3D打印所用原料密度为0.9 g/cm3，不考虑打印损耗，制作该模型所需原料的质量为___________g.‎ ‎5．【2019年高考江苏卷】如图，长方体的体积是120，E为的中点，则三棱锥E−BCD的体积是 .‎ ‎6.【2018年全国卷Ⅲ理】设A、B、C、D是同一个半径为4的球的球面上四点，为等边三角形且其面积为，则三棱锥体积的最大值为( )‎ A． B． C． D．‎ ‎2.练模拟 ‎1.【2020届安徽省合肥市高三质量检测】已知几何体的三视图如图，则该几何体的体积为( )‎ A. B. 4 C. D. ‎ ‎2.【湖南省长沙市湖南师范大学附属中学2020届高三月考】如图所示是某几何体的三视图，则该几何体的表面积为( )‎ A．57＋24π B．57＋15π C．48＋15π D．48＋24π ‎3. 【福建省福州市2020届高三质检】 “圆材埋壁”是我国古代数学著作《九章算术》中的一个问题：“今有圆材，埋在壁中，不知大小．以锯锯之，深一寸，锯道长一尺．问径几何．”用现在的数学语言表述是：“如图所示，一圆柱形埋在墙壁中，尺，为的中点，，寸，则圆柱底面的直径长是_________寸”．(注：l尺=10寸)‎ ‎4.【安徽省黄山市2020届高三一模】已知三棱锥，且均为等边三角形，二面角的平面角为60°，则三棱锥外接球的表面积是_______________.‎ ‎5.【2020届安徽省合肥市高三质量检测】已知圆锥的顶点为，母线，所成角的余弦值为，与圆锥底面所成角为45°，若的面积为，则该圆锥的侧面积为__________．‎ ‎3.练原创 ‎1．如图是一个几何体的三视图，则该几何体的表面积为 A．46 B．48‎ C．50 D．52‎ ‎2. 将边长为的正方形沿对角线折起，使为正三角形，则三棱锥的体积为( )‎ A． B． C． D． ‎ ‎3．《孙子算经》是我国古代内容极其丰富的数学名著，书中有如下问题：“今有圆窖周五丈四尺，深一丈八 尺，问受粟几何？”其意思为：“有圆柱形容器，底面圆周长五丈四尺，高一丈八尺，求此容器能放多少斛米”(古制1丈=10尺，1斛=1.62立方尺，圆周率)，则该圆柱形容器能放米______斛．‎ ‎4．在三棱锥中，平面平面，是边长为6的等边三角形，是以为斜边的等腰直角三角形，则该三棱锥外接球的表面积为_______．‎ ‎5．如图，是以为直径的半圆上异于的一点，矩形所在平面垂直于该半圆所在的平面，且．‎ ‎(1)求证：；‎ ‎(2)设平面与半圆弧的另一个交点为，，求三棱锥的体积．‎