- 2021-06-15 发布 |
- 37.5 KB |
- 7页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
贵州省兴仁市凤凰中学2019-2020学年高二上学期第二次月考数学(文)试题
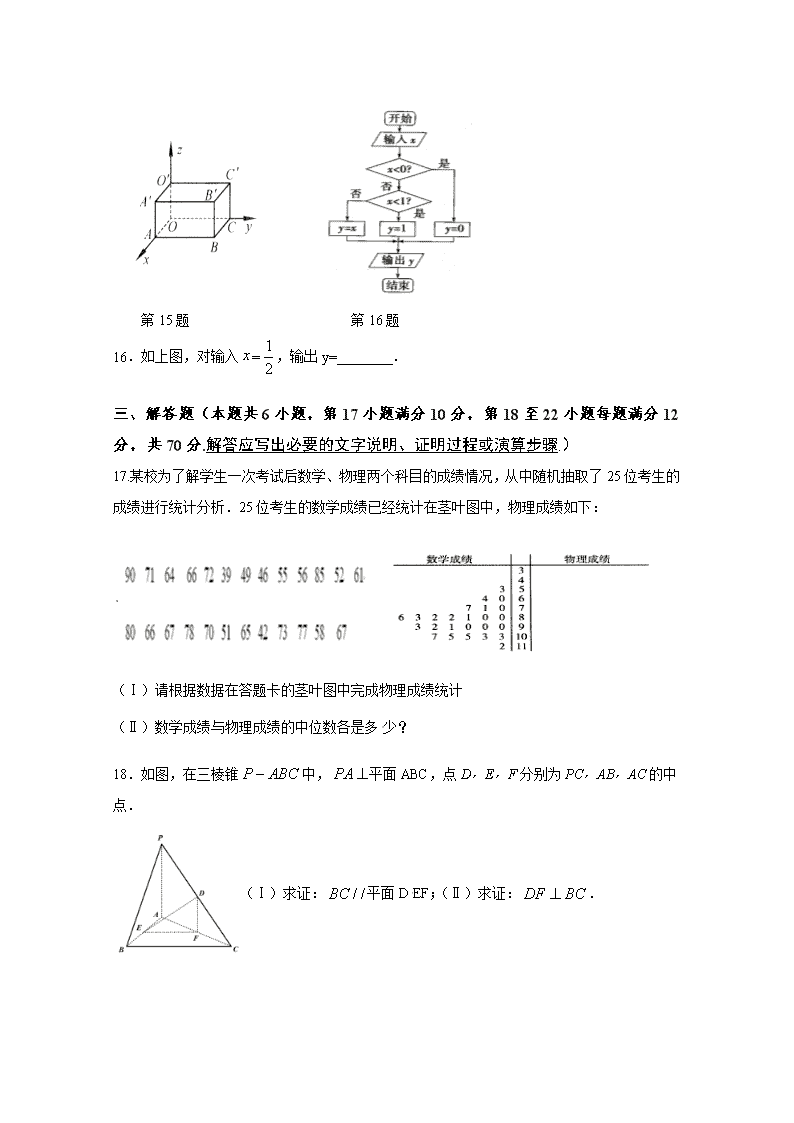
兴仁市凤凰中学2021届高二第一学期第二次月考(文)数学试卷 满分:150分 测试时间:120分钟 第I卷(选择题,共60分) 一、单选题(本题共12小题每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的) 1.直线经过点和,则直线的斜率为 A.-2 B.-1 C.1 D.2 2.已知直线,,若,则 A. B. C. D. 3.如果方程表示圆,则的取值范围是 A. B. C. D. 4.直线与圆的位置关系为 A.相离 B.相交 C.相切 D.相交或相切 5.直线在x轴,y轴上的截距分别为 A.2,3 B.-2,3 C.-2,-3 D.2,-3 6.如图所示程序框图,若判断框内为“”,则输出 A.2 B.6 C.10 D.34 7.从编号为001,002,…,460的460个产品中用系统抽样的方法抽取一个样本,己知样本中编号最小的两个编号分别为007,030,则样本中第5个产品的编号应该为 A.099 B.122 C.145 D.168 8.圆与圆的位置关系为 A.相离 B.相交 C.外切 D.内切 9.从编号为00到29的30个个体中抽取10个样本,现给出某随机数表的第11行到第15行(见下表),如果某人选取第12行的第6列的数作为第一个数并且由此数向右读,则选取的前4个的号码分别为 9264 4607 2021 3920 7766 3817 3256 1640[来源:Z*xx*k.Com] 5858 7766 3170 0500 2593 0545 5370 7814 2889 6628 6757 8231 1589 0062 0047 3815 5131 8186 3709 4521 6665 5325 5383 2702 9055 7196 2172 3207 1114 1384 4359 4488 A.76,63,17,00 B.16,00,02,30 C.17,00,02,25 D.17,00,02,07 10.若圆关于直线:对称,则直线在轴上的截距为 A.-l B.l C.3 D.-3 11.过点(3,1)作圆(x-2)2+(y-2)2=4的弦,则最短弦的长为 A.2 B. C. D.4 12.已知三点,,,则ΔABC外接圆的圆心到原点的距离为 A. B. C. D. [来源:学科网ZXXK] 第Ⅱ卷 (非选择题,共90分) 二、填空题(本题共4小题,每题5分,共20分.把答案填写在答题卡相应的位置上) 13.若圆与圆相交,则公共弦长等于__________. 14.某校共有学生2400人,其中高三年级600人.为了解各年级学生的兴趣爱好情况,用分层抽样的方法从全校学生中抽取容量为100的样本,则高三年级应抽取的学生人数为_______. 15.如图,在长方体中,,,,写出点,的坐标. 第15题 第16题 16.如上图,对输入=,输出y=________. 三、 解答题(本题共6小题,第17小题满分10分,第18至22小题每题满分12分,共70分.解答应写出必要的文字说明、证明过程或演算步骤.) 17.某校为了解学生一次考试后数学、物理两个科目的成绩情况,从中随机抽取了25位考生的成绩进行统计分析.25位考生的数学成绩已经统计在茎叶图中,物理成绩如下: (Ⅰ)请根据数据在答题卡的茎叶图中完成物理成绩统计 (Ⅱ)数学成绩与物理成绩的中位数各是多少? 18.如图,在三棱锥中,平面ABC,点D,E,F分别为PC,AB,AC的中点. (Ⅰ)求证:平面DEF;(Ⅱ)求证:. 19、若过直线与直线的交点作直线,使点,到直线的距离相等,求直线的方程. 20、经统计,某校学生上学路程所需要时间全部介于与之间(单位:分钟).现从在校学生中随机抽取人,按上学所学时间分组如下:第组,第组,第组,第组,第组,得打如图所示的频率分布直方图. (Ⅰ)根据图中数据求的值. (Ⅱ)若从第,,组中用分成抽样的方法抽取人参与交通安全问卷调查,应从这三组中各抽取几人? 21.从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量表得如下频数分布表: 质量指标值分组 [75,85) [85,95) [95,105) [105,115) [115,125) 频数 6 26 38 22 8 (I)在答题卡上作出这些数据的频率分布直方图: (II)估计这种产品质量指标值的平均数及方差(同一组中的数据用该组区间的中点值作代表);[来源:学科网] 22、已知圆的方程为.[来源:Zxxk.Com] (I)求过点的圆的切线方程. (II)求平行于直线且被圆截得的弦长为的直线方程. 兴仁市凤凰中学2021届第一学期第二次月考(文数)试题 参考答案 一、选择题: 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 C A B A D D A D D A C[来源:学§科§网Z§X§X§K] B 二、填空题: 13、 14、25 15、(3,0,2) (3,4,2) 16、1 三、 计算题 17、(Ⅰ) (Ⅱ)数学的中位数:86 物理成绩的中位数:66 18.(Ⅰ)证明:在中,因为E,F分别为AB,AC的中点,所以 因为平面DEF,平面DEF,所以平面DEF. (Ⅱ)证明:因为平面ABC,平面ABC,所以. 因为D,F分别为PC,AC的中点,所以.所以. 19、联立两直线方程得直线与直线的交点为. 分两种情况:①直线l过线段AB的中点,则直线l的方程为; ②直线l与直线AB平行,则 故直线l的方程为, 综上,直线方程为,或 20.(Ⅰ), . (Ⅱ)第组人数为人, 第组人数为人, 第组人数为人, ∴比例为, ∴第组,组,组各抽,,人. 21.(Ⅰ) (Ⅱ)=100 =100 22、(I)设切线方程, 整理得, 圆心,半径, ∴圆心到切线距离, 解出, 即切线方程为, 当切线斜率不存在时,切线平行于轴, 切线方程为,符合要求, 综上,切线方程为或. (II)设直线方程, 圆心到直线的距离, , 代入解出, ∴直线方程为 或.查看更多