- 2021-06-15 发布 |
- 37.5 KB |
- 12页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
数学理卷·2018届云南省昆明市黄冈实验学校高二上学期期中考试(2016-11)
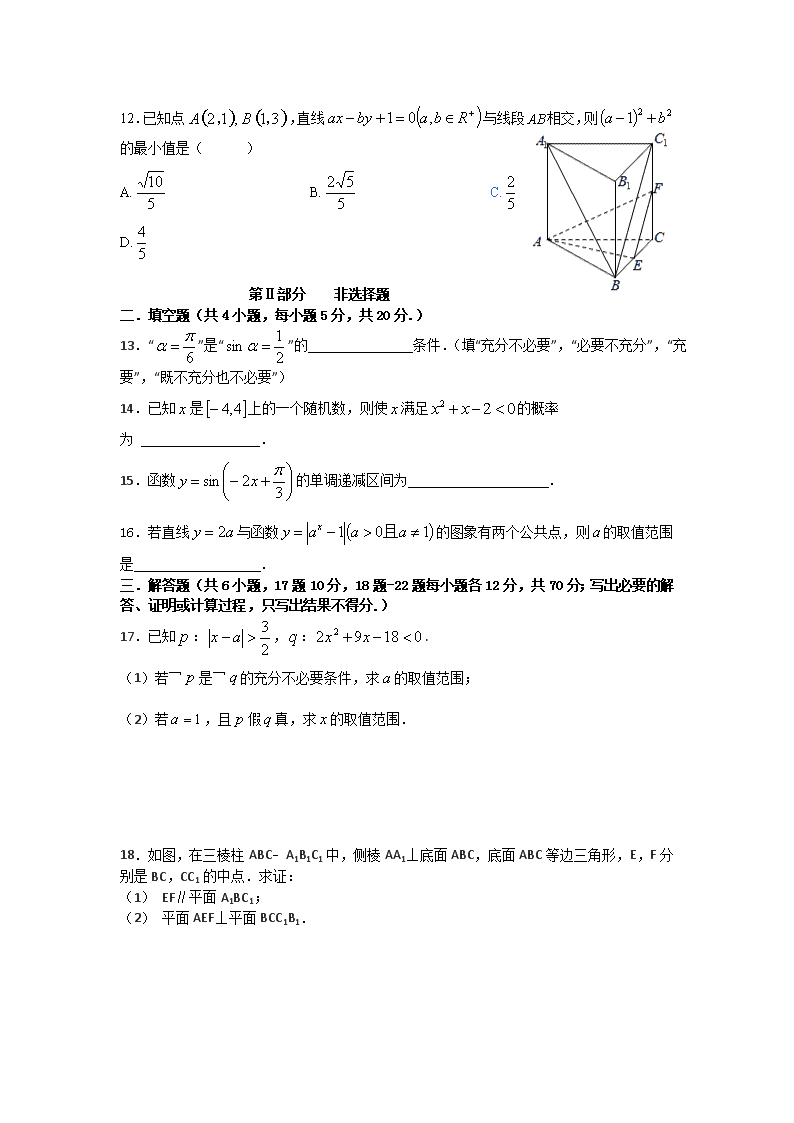
学校: 班级: 考场: 姓名: 考号: 座号: 密 封 线 内 不 准 答 题 昆明黄冈实验学校2016-2017学年度上学期期中考试 高二理科 数学试卷 第Ⅰ部分 选择题 一. 选择题(共12小题,每小题5分,共60分。每个小题的四个选项中只有一个选项符合题目要求) 1.已知命题:,总有,则¬为( ) A.,使得 B.,使得 C.,总有 D.,总有 2.“若,则全为”的逆否命题是( ) A.若,全不为,则 B.若,不全为,则 C.若,不全为,则 D.若,全为,则 3.如图1,一个四棱锥的底面为正方形,其三视图如图所示,则这个四棱锥的体积是( ) A.1 B.2 C.3 D.4 第4题图 图2 4.根据如图2的框图,当输入为6时,输出的( ) A.1 B.2 C.5 D.10 5.函数的零点所在区间是( ) A.(,1) B.(1,e﹣1) C.(e﹣1,2) D.(2,e) 第3题图 图1 6.已知点,则线段MN的垂直平分线方程为( ) A. B.C. D. 第7题图 图3 7.如图3,在□中,,点在边上,且,则 等于( ) A. B. C. D. 8.光线从点射到轴上的B点后,被轴反射,这时反射光线恰好过点,则光线BC所在直线的倾斜角为( ) A. B. C. D. 第9题图 图4 9.如右图4所示,点P在正方形ABCD所在平面外,PA⊥平面ABCD,PA=AB,则PB与AC所成的角是( ) A.90° B.60° C.45° D.30° 10.已知函数,若,则 的大小关系为( ) A. B. C. D. 11.已知函数,其图象相邻的两条对称轴方程为与,则( ) A.的最小正周期为,且在上为单调递增函数 B.的最小正周期为,且在上为单调递减函数 C.的最小正周期为, 且在上为单调递增函数 D.的最小正周期为, 且在上为单调递减函数 12.已知点,直线与线段相交,则的最小值是( ) A. B. C. D. 第Ⅱ部分 非选择题 二.填空题(共4小题,每小题5分,共20分.) 13.“”是“”的 条件.(填“充分不必要”,“必要不充分”,“充要”,“既不充分也不必要”) 14.已知是上的一个随机数,则使满足的概率为 . 15.函数的单调递减区间为 . 16.若直线与函数的图象有两个公共点,则的取值范围是 . 三.解答题(共6小题,17题10分,18题-22题每小题各12分,共70分;写出必要的解答、证明或计算过程,只写出结果不得分.) 17.已知:,:. (1)若¬是¬的充分不必要条件,求的取值范围; (2)若,且假真,求的取值范围. 18.如图,在三棱柱ABC﹣A1B1C1中,侧棱AA1⊥底面ABC,底面ABC等边三角形,E,F分别是BC,CC1的中点.求证: (1) EF∥平面A1BC1; (2) 平面AEF⊥平面BCC1B1. 19.某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生的平均分是85,乙班学生成绩的中位数是83. (1)求和的值; (2)计算甲班7位学生成绩的方差; (3)从成绩在90分以上的学生中随机抽取两名学生,求甲班至少有一名学生的概率. 20.已知圆C经过A(1,3),B(﹣1,1)两点,且圆心在直线上. (1)求圆C的方程; (2)设直线经过点(2,﹣2),且与圆C相交所得弦长为,求直线的方程. 21.已知,满足. (1) 将表示为的函数,求函数的最小正周期; (2) 已知分别为的三个内角对应的边长,的最大值是,且,求的取值范围. 22.设数列的前项和为,已知. (1)求的通项公式; (2)若数列,满足,求的前项和. 昆明黄冈实验学校2016-2017学年度上学期期中考试 高二理科数学 参考答案 一、选择题(共12小题,每小题5分,共60分。) 题号 1 2 3 4 5 6 7 8 9 10 11 12 选项 B C B D C B D B B B C C 1.解:根据全称命题的否定为特称命题可知,¬p为∃x0>0,使得(x0+1)e≤1, 故选:B. 2.解:依题意得,原命题的题设为若x2+y2=0,结论为则x,y全为零. 逆否命题:若x,y不全为零,则x2+y2≠0,故选C. 3.解:由题设及图知,此几何体为一个四棱锥,其底面为一个对角线长为2的正方形,故其底面积为=2 由三视图知其中一个侧棱为棱锥的高,其相对的侧棱与高及底面正方形的对角线组成一个直角三角形,由于此侧棱长为,对角线长为2,故棱锥的高为=3 此棱锥的体积为=2故选B. 4.解:模拟执行程序框图,可得 x=6 x=3 满足条件x≥0,x=0 满足条件x≥0,x=﹣3 不满足条件x≥0,y=10 输出y的值为10.故选:D. 5.解:∵f(e﹣1)=lne﹣=1﹣=<0, f(2)=ln3﹣1>lne﹣1=0, ∴函数f(x)=ln(x+1)﹣的零点所在区间是 (e﹣1,2), 故选C. 6.解:由中点坐标公式可得M,N的中点为(1,4), 可得直线MN的斜率为k===﹣1, 由垂直关系可得其垂直平分线的斜率为k′=1, 故可得所求直线的方程为:y﹣4=1×(x﹣1), 化为一般式可得x﹣y+3=0故选B. 7. 解:根据题意及图形, 故选D 8.解:点A关于x轴的对称点为A′(﹣2,﹣), A′在直线BC上, ∴直线BC的斜率是 kBC===; ∴直线BC的倾斜角是. 故选:B. 9.解:将其还原成正方体ABCD﹣PQRS,连接SC,AS,则PB∥SC, ∴∠ACS(或其补角)是PB与AC所成的角 ∵△ACS为正三角形, ∴∠ACS=60° ∴PB与AC所成的角是60° 故选B. 10.解:设k=,则k的几何意义为图象f(x)上的点(x,y)与原点的斜率, 作出函数f(x)的图象, 当0<c<b<a时, 由图象知k0C>k0B>k0A, 即>>, 故选:B. 11.解:∵f(x)=sin(ωx+φ)﹣cos(ωx+φ) =sin(ωx+φ﹣)(ω>0,|φ|<2π), ∵图象相邻的两条对称轴方程为x=0与x=, ∴T=π,∴ω=2, ∵对称轴方程为x=0, ∴f(0)=或f(0)=﹣, sin(φ﹣)=1或﹣1, ∵|φ|<,∴φ=﹣, ∴f(x)=sin(2x﹣), ∴f(x)的最小正周期为π, 当x∈(0,)时,2x﹣∈(﹣,), 且在(0,)上为单调递增. 故选:C 12.解:由已知有,作出可行域, 令,则d的几何意义为平面区域内的点到点(1,0)的距离, 由图象可知d的最小值为点(1,0)到直线a-3b+1=0的距离,此时, ∴的最小值为,故选C. 二、填空题(共4小题,每小题5分,共20分。) 13. 充分不必要 14. 15. 16. 13.解:∵α=30⇒sinα=0.5,又当sinα=0.5时,α=+kπ, ∴sinα=0.5推不出α=30°, ∴α=30°是“sinα=0.5”的充分不必要条件, 故答案为充分不必要条件. 14.解:x对应的所有结果构成的区间长度是4﹣(﹣4)=8 ∵x2+x﹣2<0∴﹣2<x<1 ∴满足x2+x﹣2<0的x构成的区间长度是1﹣(﹣2)=3 由几何概型概率公式得P=,故答案为 15.解:由于函数=﹣sin(2x﹣),本题即求函数t=sin(2x﹣)的增区间. 令2kπ﹣≤2x﹣≤2kπ+,k∈z,可得 kπ﹣≤x≤kπ+, 故函数的单调递减区间为kπ﹣,kπ+], 故答案为kπ﹣,kπ+],k∈z. 16.解:当0查看更多