【数学】2019届一轮复习人教A版(文)二元一次不等式(组)及简单的线性规划问题学案
第3讲 二元一次不等式(组)及简单的线性规划问题
板块一 知识梳理·自主学习
[必备知识]
考点1 判断二元一次不等式表示的平面区域
由于对直线Ax+By+C=0同一侧的所有点(x,y),把它的坐标(x,y)代入Ax+By+C所得到实数的符号都相同,所以只需在此直线的某一侧取一个特殊点(x0,y0),由Ax0+By0+C的符号即可判断Ax+By+C>0表示直线Ax+By+C=0哪一侧的平面区域.
考点2 线性规划中的基本概念
名称
定义
约束条件
由变量x,y组成的不等式(组)
线性约束条件
关于x,y的一次不等式(或等式)
目标函数
关于x,y的函数解析式,如z=2x+3y等
续表
名称
定义
线性目标函数
关于x,y的一次解析式
可行解
满足线性约束条件的解(x,y)
可行域
所有可行解组成的集合
最优解
使目标函数取得最大值或最小值的可行解
线性规划问题
在线性约束条件下求线性目标函数的最大值或最小值问题
[必会结论]
画二元一次不等式表示的平面区域的方法
(1)直线定界:不等式中无等号时直线画成虚线,有等号时直线画成实线;
(2)特殊点定域:若直线不过原点,特殊点常选原点;若直线过原点,则特殊点常选取(0,1)或(1,0)来验证.
[考点自测]
1.判断下列结论的正误.(正确的打“√”,错误的打“×”)
(1)不等式Ax+By+C>0表示的平面区域一定在直线Ax+By+C=0的上方.( )
(2)任何一个二元一次不等式组都表示平面上的一个区域.( )
(3)线性目标函数的最优解可能是不唯一的.( )
(4)目标函数z=ax+by(b≠0)中,z的几何意义是直线ax+by-z=0在y轴上的截距.( )
答案 (1)× (2)× (3)√ (4)×
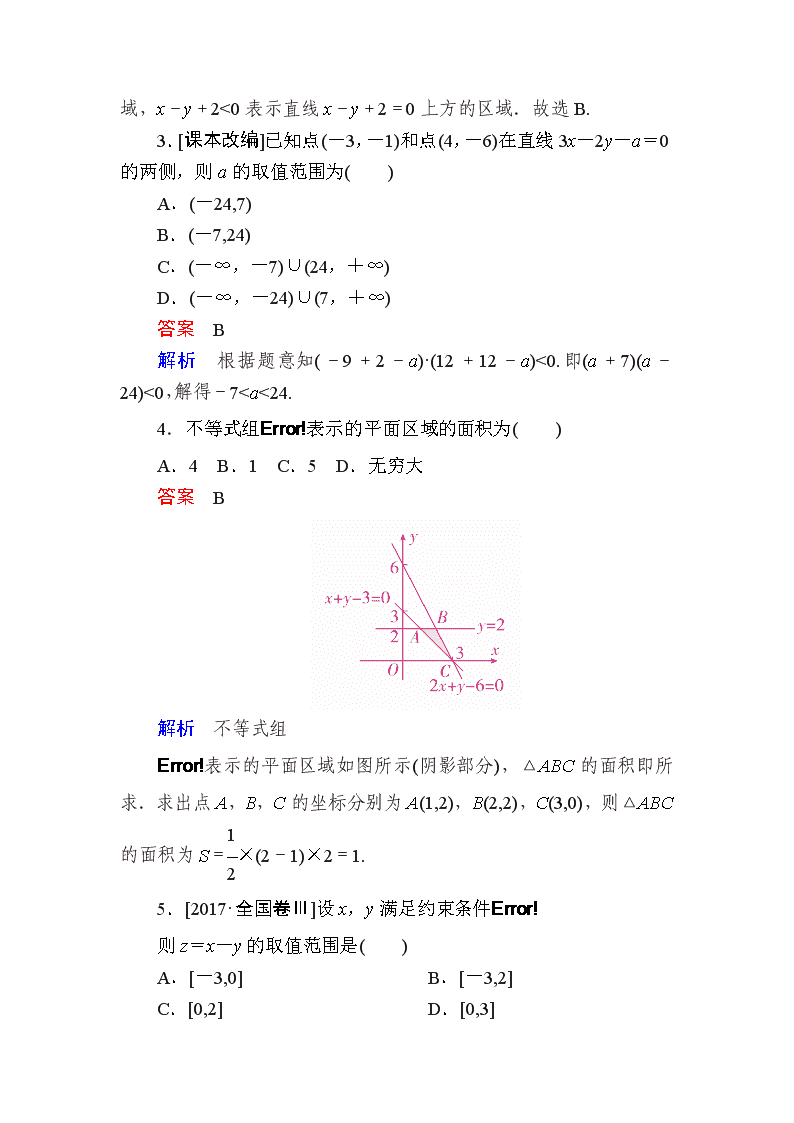
2.[2018·吉林长春模拟]不等式组表示的平面区域是( )
答案 B
解析 x-3y+6≥0表示直线x-3y+6=0
以及该直线下方的区域,x-y+2<0表示直线x-y+2=0上方的区域.故选B.
3.[课本改编]已知点(-3,-1)和点(4,-6)在直线3x-2y-a=0的两侧,则a的取值范围为( )
A.(-24,7)
B.(-7,24)
C.(-∞,-7)∪(24,+∞)
D.(-∞,-24)∪(7,+∞)
答案 B
解析 根据题意知(-9+2-a)·(12+12-a)<0.即(a+7)(a-24)<0,解得-7
0时,如图1所示,此时可行域为x轴上方、直线x+y-2=0的右上方、直线kx-y+2=0的右下方的区域,显然此时z=y-x无最小值.
当k<-1时,z=y-x取得最小值2;当k=-1时,z=y-x取得最小值-2,均不符合题意.
当-10时,截距取最大值时,z也取最大值;截距取最小值时,z也取最小值;当b<0时,截距取最大值时,z取最小值;截距取最小值时,z取最大值.
板块三 启智培优·破译高考
题型技法系列9——非线性目标函数的最值问题
[2016·江苏高考]已知实数x,y满足
则x2+y2的取值范围是________.
解题视点 本题中x2+y2的几何意义是点(x,y)
到原点的距离的平方,不能遗漏平方.
解析 不等式组所表示的平面区域是以点(0,2),(1,0),(2,3)为顶点的三角形及其内部,如图所示.因为原点到直线2x+y-2=0的距离为,所以(x2+y2)min=,又当(x,y)取点(2,3)时,x2+y2取得最大值13,故x2+y2的取值范围是.
答案
答题启示 与二元一次不等式(组)表示的平面区域有关的非线性目标函数的最值问题的求解一般要结合给定代数式的几何意义来完成.常见代数式的几何意义:(1)表示点(x,y)与原点(0,0)的距离;(2)表示点(x,y)与点(a,b)之间的距离;(3)表示点(x,y)到直线Ax+By+C=0的距离;(4)表示点(x,y)与原点(0,0)连线的斜率;(5)表示点(x,y)与点(a,b)连线的斜率.
跟踪训练
[2018·成都模拟]设实数x,y满足不等式组
则ω=的取值范围是( )
A. B.
C. D.
答案 B
解析 作出不等式组所表示的可行域,如图中阴影部分所示,由于可以看作直线的斜率形式,于是问题可以转化为求可行域内的哪些点与点A(-1,1)连线的斜率最大、最小问题.
如图,当直线过点B(1,0)时,斜率最小,此时ω==-;
当直线与x-y=0平行时,斜率最大,此时ω=1,但它与阴影区域无交点,取不到.
故ω=的取值范围是.故选B.
板块四 模拟演练·提能增分
[A级 基础达标]
1.[2017·北京高考]若x,y满足则x+2y的最大值为( )
A.1 B.3 C.5 D.9
答案 D
解析 作出可行域如图阴影部分所示.
设z=x+2y,则y=-x+z.
作出直线l0:y=-x,并平移该直线,可知当直线y=-x+z过点C时,z取得最大值.
由得故C(3,3).
∴zmax=3+2×3=9.故选D.
2.[2017·浙江高考]若x,y满足约束条件
则z=x+2y的取值范围是( )
A.[0,6] B.[0,4]
C.[6,+∞) D.[4,+∞)
答案 D
解析 作出不等式组表示的平面区域,如图中阴影部分所示.
由题意可知,当直线y=-x+过点A(2,1)时,z取得最小值,即zmin=2+2×1=4.所以z=x+2y的取值范围是[4,+∞).故选D.
3.[2018·陕西黄陵中学模拟]已知变量x,y满足约束条件目标函数z=x+2y的最大值为10,则实数a的值等于( )
A.4 B. C.2 D.8
答案 A
解析 由不等式组可得可行域如图中阴影部分所示,当直线z=x+2y经过点A(a,a-1)时,z取得最大值,由已知得a+2(a-1)=10,解得a=4.故选A.
4.[2018·开封模拟]设变量x,y满足约束条件
则目标函数z=x2+y2的取值范围为( )
A.[2,8] B.[4,13]
C.[2,13] D.
答案 C
解析 作出可行域,如图中阴影部分,将目标函数看作是可行域内的点到原点的距离的平方,从而可得zmin=|OA|2=2=2,zmax=|OB|2=32+22=13.故z的取值范围为[2,13].
5.[2015·陕西高考]某企业生产甲、乙两种产品均需用A,B两种原料,已知生产1吨每种产品所需原料及每天原料的可用限额如表所示.如果生产1吨甲、乙产品可获利润分别为3万元、4万元,则该企业每天可获得最大利润为( )
甲
乙
原料限额
A(吨)
3
2
12
B(吨)
1
2
8
A.12万元 B.16万元 C.17万元 D.18万元
答案 D
解析 设该企业每天生产甲产品x吨,乙产品y吨,获利z元.
则由题意知利润函数z=3x+4y.
画出可行域如图所示,当直线3x+4y-z=0过点B时,目标函数取得最大值.由
解得
故利润函数的最大值为z=3×2+4×3=18(万元).故选D.
6.某校今年计划招聘女教师a名,男教师b名,若a,b满足不等式组设这所学校今年计划招聘教师最多x名,则x=( )
A.10 B.12 C.13 D.16
答案 C
解析 画出约束条件所表示的区域,即可行域,如图阴影部分所示,作直线l:b+a=0,平移直线l,再由a,b∈N,可知当a=6,b=7时,x=a+b=13.故选C.
7.[2017·全国卷Ⅰ]设x,y满足约束条件
则z=3x-2y的最小值为________.
答案 -5
解析 作出可行域如图阴影部分所示.
由z=3x-2y,得y=x-.
作出直线l0:y=x,并平移l0,知当直线y=x-过点A时,z取得最小值.
由得A(-1,1),
∴zmin=3×(-1)-2×1=-5.
8.[2018·辽宁模拟]设变量x,y满足则2x+3y的最大值为________.
答案 55
解析 不等式组表示的区域如图所示,令z=2x+3y,目标函数变为y=-x+,因此截距越大,z的取值越大,故当直线z=2x+3y
经过点A时,z最大,由于⇒故点A的坐标为(5,15),代入z=2x+3y,得到zmax=55,即2x+3y的最大值为55.
9.已知变量x,y满足约束条件且有无穷多个点(x,y)使目标函数z=x+my取得最小值,求m的值.
解 作出线性约束条件表示的平面区域,如图中阴影部分所示.
若m=0,则z=x,目标函数z=x+my取得最小值的最优解只有一个,不符合题意.
若m≠0,则目标函数z=x+my可看作斜率为-的动直线y=-x+,
若m<0,则->0,数形结合知使目标函数z=x+my取得最小值的最优解不可能有无穷多个;
若m>0,则-<0,数形结合可知,当动直线与直线AB重合时,有无穷多个点(x,y),在线段AB上,使目标函数z=x+my取得最小值,即-=-1,则m=1.
综上可知,m=1.
10.变量x,y满足
(1)设z=,求z的最小值;
(2)设z=x2+y2,求z的取值范围;
(3)设z=x2+y2+6x-4y+13,求z的取值范围.
解 由约束条件
作出(x,y)的可行域如图所示.
由
解得A.
由
解得C(1,1).
由解得B(5,2).
(1)因为z==,
所以z的值即是可行域中的点与原点O连线的斜率.观察图形可知zmin=kOB=.
(2)z=x2+y2的几何意义是可行域上的点到原点O的距离的平方.结合图形可知,可行域上的点到原点的距离中,dmin=|OC|=,dmax=|OB|=.所以2≤z≤29.
(3)z=x2+y2+6x-4y+13=(x+3)2+(y-2)2的几何意义是可行域上的点到点(-3,2)的距离的平方.结合图形可知,可行域上的点到
(-3,2)的距离中,dmin=1-(-3)=4,dmax==8.所以16≤z≤64.
[B级 知能提升]
1.[2018·南昌调研]设变量x,y满足约束条件
则z=|x-3y|的最大值为( )
A.10 B.8 C.6 D.4
答案 B
解析 不等式组
所表示的平面区域如图中阴影部分所示.
当平移直线x-3y=0过点A时,m=x-3y取最大值;
当平移直线x-3y=0过点C时,m=x-3y取最小值.
由题意可得A(-2,-2),C(-2,2),所以mmax=-2-3×(-2)=4,mmin=-2-3×2=-8,
所以-8≤m≤4,所以|m|≤8,即zmax=8.
2.若不等式组表示的平面区域为三角形,且其面积等于,则m的值为( )
A.-3 B.1 C. D.3
答案 B
解析 作出可行域,如图中阴影部分所示,
易求A,B,C,D的坐标分别为A(2,0),
B(1-m,1+m),
C,
D(-2m,0).S△ABC=S△ADB-S△ADC=|AD|·|yB-yC|=(2+2m)=(1+m)·=,解得m=1或m=-3(舍去).
3.实数x,y满足不等式组则z=|x+2y-4|的最大值为________.
答案 21
解析 作出不等式组表示的平面区域,如图中阴影部分所示.z=|x+2y-4|=·,即其几何含义为阴影区域内的点到直线x+2
y-4=0的距离的倍.
由得B点坐标为(7,9),显然点B到直线x+2y-4=0的距离最大,此时zmax=21.
4.[2018·德州检测]若x,y满足约束条件
(1)求目标函数z=x-y+的最值;
(2)若目标函数z=ax+2y仅在点(1,0)处取得最小值,求a的取值范围.
解 (1)作出可行域如图,可求得A(3,4),B(0,1),C(1,0).
平移初始直线x-y+=0,可知z=x-y+过A(3,4)时取最小值-2,过C(1,0)时取最大值1.
所以z的最大值为1,最小值为-2.
(2)直线ax+2y=z仅在点(1,0)处取得最小值,由图象可知-1<-<2,解得-4
查看更多