- 2021-06-15 发布 |
- 37.5 KB |
- 17页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
陕西省汉中龙岗学校2019-2020学年高一上学期期末考试数学试题 含解析
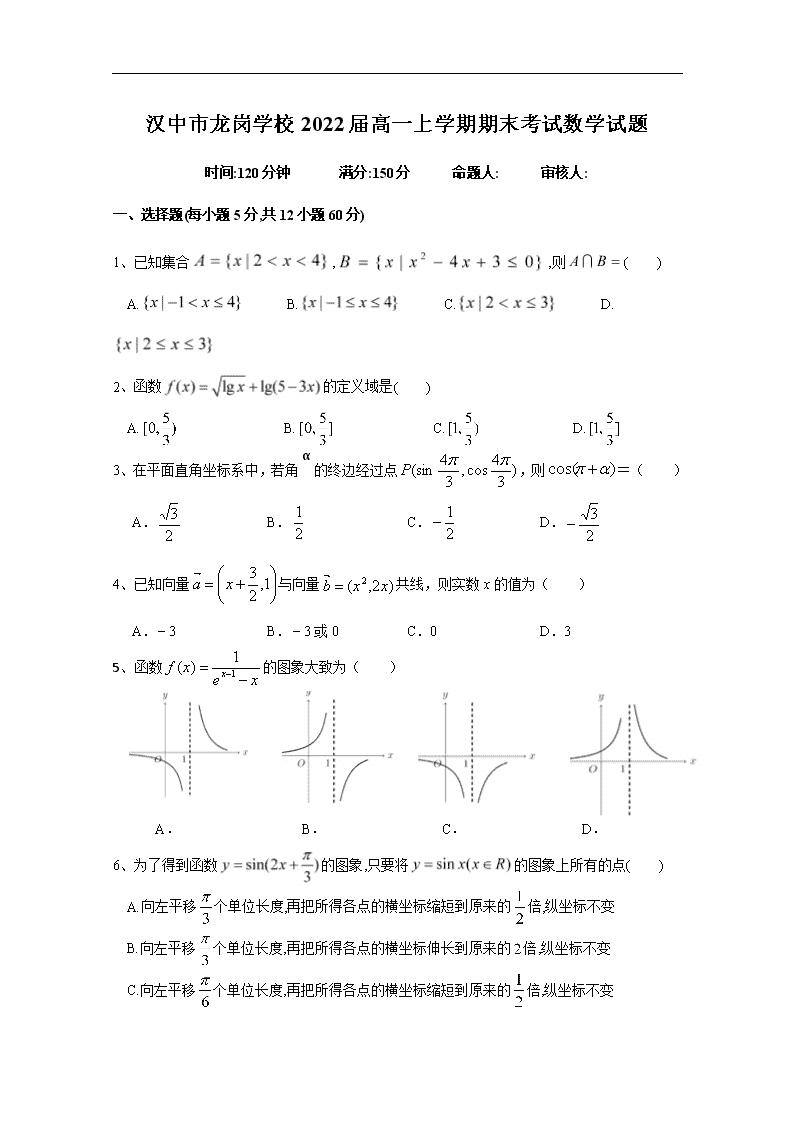
汉中市龙岗学校2022届高一上学期期末考试数学试题 时间:120分钟 满分:150分 命题人: 审核人: 一、选择题(每小题5分,共12小题60分) 1、已知集合,,则( ) A. B. C. D. 2、函数的定义域是( ) A. B. C. D. 3、在平面直角坐标系中,若角α的终边经过点,则=( ) A. B. C. D. 4、已知向量与向量共线,则实数x的值为( ) A. B.或0 C.0 D.3 5、函数的图象大致为( ) A. B. C. D. 6、为了得到函数的图象,只要将的图象上所有的点( ) A.向左平移个单位长度,再把所得各点的横坐标缩短到原来的倍,纵坐标不变 B.向左平移个单位长度,再把所得各点的横坐标伸长到原来的倍,纵坐标不变 C.向左平移个单位长度,再把所得各点的横坐标缩短到原来的倍,纵坐标不变 D.向左平移个单位长度,再把所得各点的横坐标伸长到原来的倍,纵坐标不变 7、下列函数f(x)中,满足“对任意x1,x2∈(0,+∞),且x1<x2都有f(x1)>f(x2)”的是( ) A. B. C.f(x)=lnx D.f(x)=x3 8、已知函数,则=( ) A.5 B. C. D. 9、如果函数的图像关于点中心对称,那么的最小值为( ) A. B. C. D. 10、已知函数,若,则实数x的取值范围为( ) A. B. C. D. 11、若函数在区间(1,e)上存在零点,则常数a的取值范围为( ) A.0<a<1 B. C. D. 12、将函数的图象向右平移个单位,在向上平移一个单位,得到的图象,若,且,,则的最大值为( ) A. B. C. D . 二、填空题(每小题5分,共4小题20分) 13、已知向量,且,则实数m= 14、若扇形的周长是,面积,则扇形圆心角的弧度数的绝对值为__________. 15、已知幂函数的图象经过点(4,2),则= . 16、在△ABC中,角A为,角A的平分线AD交BC于点D,已知,且,则在方向上的投影是 . 三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。 17、(本大题满分10分) 计算(1); (2)解方程: 18、已知向量 (1)若,求的值; (2)若,,求的值. 19、(本大题满分12分) 已知函数在区间[2,3]上的最小值为1. (1)求a的值; (2)若存在x0使得不等式在成立,求实数k的取值范围. 20、(本大题满分12分) 已知函数,x∈R (1)求函数的最小正周期和单调递增区间; (2)求函数在区间上的最小值和最大值,并求出取得最值时x的值. 21、(本大题满分12分) 已知某帆船中心比赛场馆区的海面上每天海浪高度(米)可看作时间(单位:小时)的函数,记作,经过长期观测,的曲线可近似地看成是函数,下列是某日各时的浪高数据. t/小时 0 3 6 9 12 15 18 21 24 y/米 1 1 1 1 (1)根据以上数据,求出的解析式; (2)为保证安全,比赛时的浪高不能高于米,则在一天中的哪些时间可以进行比赛. 22、(本大题满分12分) 已知函数是偶函数. (1)求的值; (2)若方程有实数根,求的取值范围; (3)设,若函数与的图象有且只有一个公共点,求实数的取值范围. 汉中市龙岗学校2022届高一上学期期末考试数学试题答案解析 一、CCABD 1、C 2、C 3、A 4、B 5、D 6、A 7、B 8、A 9、A 10、A 11、C 12、A 13、±4 14、 15、 16、 17、(1)原式 (2) ∴ 18、解:(Ⅰ)时,, ∴, ∴; (Ⅱ)∵, ∴, ∴, ∴,且α∈(0,π),∴sinα>0, ∴解得,, ∴=. 19、解:(1)f(x)=(x﹣a)2+1﹣a2, 当a<2时,f(x)min=f(2)=5﹣4a=1,解得a=1, 当2≤a≤3时,f(x)min=f(a)=1﹣a2=1,解得a=0不符合题意, 当a>3时,f(x)min=f(3)=10﹣6a=1,解得a=,不符合题意. 综上所述,a=1. (2)因为⇒, 可化为1+()2﹣2•<k, 令t=,则k>t2﹣2t+1, 因x∈[﹣1,1],故t∈[,3].故k>t2﹣2t+1在t∈[,3]上有解, 记h(t)=t2﹣2t+1=(t﹣1)2,t∈[,3],故h(t)min=h(1)=0, 所以k的取值范围是(0,+∞). 21、(1)由表中数据可以看到浪高最大值为,最小值为, ∴,, 又∵相隔小时达到一次最大值,说明周期为, ∴,, 即. (2)由题意知,当时,比赛才能进行,即, ∴,, 解得, 又∵,∴当时,;当时,, 故比赛安全进行的时间段为 22、(1)∵为偶函数,∴,有, ∴对恒成立. ∴对恒成立, ∴对恒成立,∴. (2)由题意知,有实数根,即有解. 令,则函数的图象与直线有交点, . ∵,∴, ∴的取值范围是. (3)由(1)知,, ∴由题意知有且只有一个实数根. 令,则,则关于的方程(*)有且只有一个正根. 若,则,不合题意,舍去; 若,则方程(*)的两根异号或方程有两相等正根. 方程(*)有两相等正根等价于,可解得. 方程(*)的两根异号等价于,可解得. 综上所述,实数的取值范围是. 汉中市龙岗学校2022届高一上学期期末考试数学试题答案解析 第1题答案 C 第1题解析 由,解得,故 . 第2题答案 C 第2题解析 函数的定义域是, 解得. 第3题答案 A 第3题解析 解:由题意可得,P(), 故cosα=, 则cos(π+α)=﹣cosα=. 故选:A. 第4题答案 B 第4题解析 向量=(x+,1)与向量=(x2,2x)共线, 则2x(x+)﹣x2=0, 即x2+3x=0, 解得x=0或x=﹣3; 所以实数x的值为﹣3或0. 第5题答案 D 第5题解析 根据题意,函数f(x)=,有ex﹣1﹣x≠0,则有x≠1,即函数的定义域为{x|x≠1}, 设t=ex﹣1﹣x,其导数t′=ex﹣1﹣1, 易得在区间(﹣∞,1)上,t′<0,t=ex﹣1﹣x为减函数,在区间(1,+∞)上,t′>0,t=ex﹣1﹣x为增函数, 则t=ex﹣1﹣x有最小值tx=1=e0﹣1=0,则有t≥0, 对于f(x)=,必有f(x)>0, 则函数f(x)的定义域为{x|x≠1}且f(x)>0, 第6题答案 A 第6题解析 将函数的图象向左平移个单位后所得到的函数图象对应的解析式为 ,再把所得各点的横坐标缩短到原来的倍, 所得到的函数图象对应的解析式为. 第7题答案 B 第7题解析 “对任意x1,x2∈(0,+∞),且x1<x2都有f(x1)>f(x2)”, ∴函数f(x)在(0,+∞)上单调递减, 结合选项可知,f(x)=在(0,+∞)单调递增,不符合题意, f(x)=2﹣x=在(0,+∞)单调递减,符合题意, f(x)=lnx在(0,+∞)单调递增,不符合题意, f(x)=x3在(0,+∞)单调递增,不符合题意, 第8题答案 A 第8题解析 根据题意,函数, 又由log2=﹣log25,则﹣3<log2=﹣log25<﹣2, 则f(log2)=f(﹣log25)=f(2﹣log25)=f(4﹣log25)=f(log2)===, 第9题答案 A 第9题解析 ∵函数的图像关于点中心对称, ∴∴由此易得. 第10题答案 A 第10题解析 f(x)是R上的偶函数, ∴f(x)在[0,+∞)上是增函数, ∴由f(2x﹣1)≥f(x)得,f(|2x﹣1|)≥f(|x|), ∴|2x﹣1|≥|x|, ∴(2x﹣1)2≥x2,解得或x≥1, ∴实数x的取值范围为. 第11题答案 C 第11题解析 解:函数在区间(1,e)上为增函数, ∵f(1)=ln1﹣1+a<0,f(e)=lne﹣+a>0, 可得<a<1 故选:C. 第12题答案 A 第12题解析 将函数的图象向右平移个单位,再向上平移一个单位, 得到的图象,故的最大值为,最小值为, 若,则或(舍去). 故有,即, 又,,则取得最大值为. 第13题答案 ±4 第13题解析 解:∵, ∴=4+m2﹣16﹣4=0,解得m=±4. 第14题答案 第14题解析 设扇形的半径为,弧长,面积为,则 ,,,, 第15题答案 第15题解析 函数y=mxn(m,n∈R)为幂函数,则m=1; 又函数y的图象经过点(4,2),则4n=2,解得n=; 所以m﹣n=1﹣=. 故答案为:. 第16题答案 第16题解析 由λ=﹣可得:=λ+, ∵B,C,D三点共线,故λ+=1,即λ=. ∴=+. 以A为原点,以AB为x轴建立平面直角坐标系如图所示,则D(3,), 设B(m,0),C(n,n), 由=+得:,解得m=3,n=3. 故B(3,0), ∴在上的投影为|AB|cos30°=. 故选:D. 第17题答案 见解析 第17题解析 (1)原式 (2) ∴ 第18题答案 见解析. 第18题解析 解:(Ⅰ)时,, ∴, ∴; (Ⅱ)∵, ∴, ∴, ∴,且α∈(0,π),∴sinα>0, ∴解得,, ∴=. 第19题答案 见解析 第19题解析 解:(1)f(x)=(x﹣a)2+1﹣a2, 当a<2时,f(x)min=f(2)=5﹣4a=1,解得a=1, 当2≤a≤3时,f(x)min=f(a)=1﹣a2=1,解得a=0不符合题意, 当a>3时,f(x)min=f(3)=10﹣6a=1,解得a=,不符合题意. 综上所述,a=1. (2)因为⇒, 可化为1+()2﹣2•<k, 令t=,则k>t2﹣2t+1, 因x∈[﹣1,1],故t∈[,3].故k>t2﹣2t+1在t∈[,3]上有解, 记h(t)=t2﹣2t+1=(t﹣1)2,t∈[,3],故h(t)min=h(1)=0, 所以k的取值范围是(0,+∞). 第20题答案 见解析 第20题解析 第21题答案 见解析 第21题解析 (1)由表中数据可以看到浪高最大值为,最小值为, ∴,, 又∵相隔小时达到一次最大值,说明周期为, ∴,, 即. (2)由题意知,当时,比赛才能进行,即, ∴,, 解得, 又∵,∴当时,;当时,, 故比赛安全进行的时间段为. 第22题答案 略 第22题解析 (1)∵为偶函数,∴,有, ∴对恒成立. ∴对恒成立, ∴对恒成立,∴. (2)由题意知,有实数根,即有解. 令,则函数的图象与直线有交点, . ∵,∴, ∴的取值范围是. (3)由(1)知,, ∴由题意知有且只有一个实数根. 令,则,则关于的方程(*)有且只有一个正根. 若,则,不合题意,舍去; 若,则方程(*)的两根异号或方程有两相等正根. 方程(*)有两相等正根等价于,可解得. 方程(*)的两根异号等价于,可解得. 综上所述,实数的取值范围是.查看更多