- 2021-06-15 发布 |
- 37.5 KB |
- 5页
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高考理科数学专题复习练习13.1算法与程序框图
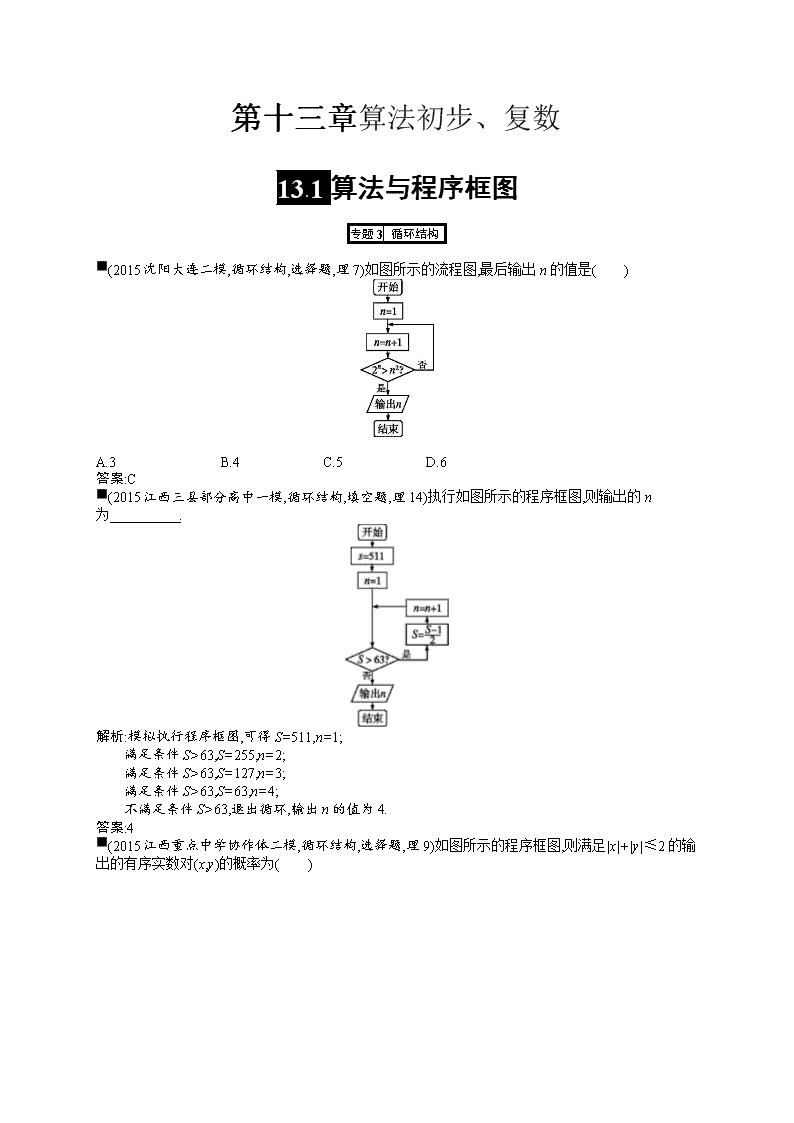
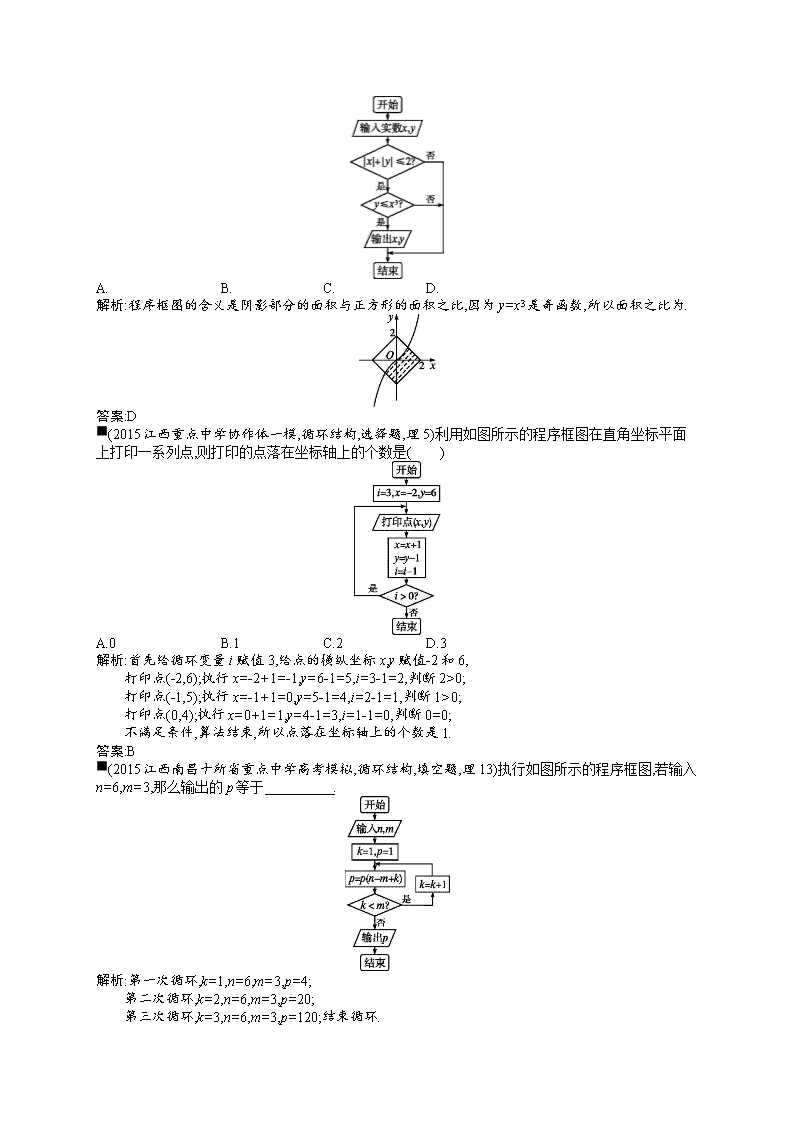
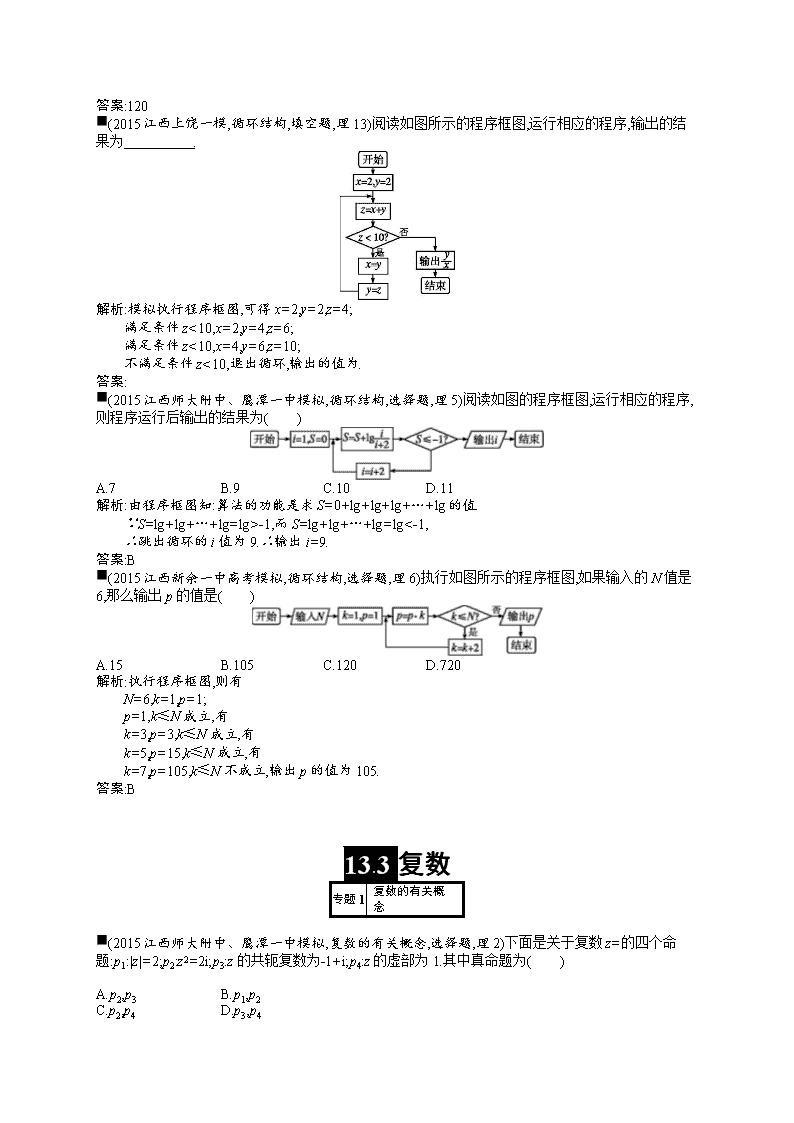
第十三章算法初步、复数 13.1算法与程序框图 专题3 循环结构 ■(2015沈阳大连二模,循环结构,选择题,理7)如图所示的流程图,最后输出n的值是( ) A.3 B.4 C.5 D.6 答案:C ■(2015江西三县部分高中一模,循环结构,填空题,理14)执行如图所示的程序框图,则输出的n为 . 解析:模拟执行程序框图,可得S=511,n=1; 满足条件S>63,S=255,n=2; 满足条件S>63,S=127,n=3; 满足条件S>63,S=63,n=4; 不满足条件S>63,退出循环,输出n的值为4. 答案:4 ■(2015江西重点中学协作体二模,循环结构,选择题,理9)如图所示的程序框图,则满足|x|+|y|≤2的输出的有序实数对(x,y)的概率为( ) A. B. C. D. 解析:程序框图的含义是阴影部分的面积与正方形的面积之比,因为y=x3是奇函数,所以面积之比为. 答案:D ■(2015江西重点中学协作体一模,循环结构,选择题,理5)利用如图所示的程序框图在直角坐标平面上打印一系列点,则打印的点落在坐标轴上的个数是( ) A.0 B.1 C.2 D.3 解析:首先给循环变量i赋值3,给点的横纵坐标x,y赋值-2和6, 打印点(-2,6);执行x=-2+1=-1,y=6-1=5,i=3-1=2,判断2>0; 打印点(-1,5);执行x=-1+1=0,y=5-1=4,i=2-1=1,判断1>0; 打印点(0,4);执行x=0+1=1,y=4-1=3,i=1-1=0,判断0=0; 不满足条件,算法结束,所以点落在坐标轴上的个数是1. 答案:B ■(2015江西南昌十所省重点中学高考模拟,循环结构,填空题,理13)执行如图所示的程序框图,若输入n=6,m=3,那么输出的p等于 . 解析:第一次循环,k=1,n=6,m=3,p=4; 第二次循环,k=2,n=6,m=3,p=20; 第三次循环,k=3,n=6,m=3,p=120;结束循环. 答案:120 ■(2015江西上饶一模,循环结构,填空题,理13)阅读如图所示的程序框图,运行相应的程序,输出的结果为 . 解析:模拟执行程序框图,可得x=2,y=2,z=4; 满足条件z<10,x=2,y=4,z=6; 满足条件z<10,x=4,y=6,z=10; 不满足条件z<10,退出循环,输出的值为. 答案: ■(2015江西师大附中、鹰潭一中模拟,循环结构,选择题,理5)阅读如图的程序框图,运行相应的程序,则程序运行后输出的结果为( ) A.7 B.9 C.10 D.11 解析:由程序框图知:算法的功能是求S=0+lg+lg+lg+…+lg的值. ∵S=lg+lg+…+lg=lg>-1,而S=lg+lg+…+lg=lg<-1, ∴跳出循环的i值为9.∴输出i=9. 答案:B ■(2015江西新余一中高考模拟,循环结构,选择题,理6)执行如图所示的程序框图,如果输入的N值是6,那么输出p的值是( ) A.15 B.105 C.120 D.720 解析:执行程序框图,则有 N=6,k=1,p=1; p=1,k≤N成立,有 k=3,p=3,k≤N成立,有 k=5,p=15,k≤N成立,有 k=7,p=105,k≤N不成立,输出p的值为105. 答案:B 13.3复数 专题1 复数的有关概念 ■(2015江西师大附中、鹰潭一中模拟,复数的有关概念,选择题,理2)下面是关于复数z=的四个命题:p1:|z|=2;p2:z2=2i;p3:z的共轭复数为-1+i;p4:z的虚部为1.其中真命题为( ) A.p2,p3 B.p1,p2 C.p2,p4 D.p3,p4 解析:复数z==1+i的四个命题: p1:|z|=≠2,是假命题; p2:z2=(1+i)2=2i,是真命题; p3:z的共轭复数为1-i,是假命题; p4:z的虚部为1,是真命题. 其中真命题为p2,p4. 答案:C ■(2015沈阳大连二模,复数的有关概念,选择题,理2)已知复数z的共轭复数为,若||=4,则z·=( ) A.4 B.2 C.16 D.±2 答案:C ■(2015江西重点中学十校二模联考,复数的有关概念,填空题,理13)设i为虚数单位,复数z=(1+i)(cos θ-i·sin θ)∈R(0<θ<π),则tan θ= . 解析:因为复数z=(1+i)(cosθ-i·sinθ)=(cosθ+sinθ)+(cosθ-sinθ)i∈R, 所以cosθ-sinθ=0,即sin=0,0<θ<π, 所以θ=. 所以tanθ=. 答案: 专题3 复数的代数运算 ■(2015江西重点中学协作体一模,复数的代数运算,选择题,理2)若复数z满足(3-4i)z=|4+3i|,则z的虚部为( ) A.-4 B.- C. D.4 解析:∵|4+3i|==5, ∴(3-4i)z=|4+3i|可化为z=i. ∴z的虚部为. 答案:C ■(2015江西南昌十所省重点中学高考模拟,复数的代数运算,选择题,理2)若(a∈R)是纯虚数,则=( ) A.i B.1 C. D.2 解析:∵是纯虚数, ∴解得a=1. ∴=1. 答案:B ■(2015江西上饶一模,复数的代数运算,选择题,理2)设z的共轭复数是,且z+=4,z·=8,则等于( ) A.±1 B.±i C.1 D.-i 解析:设z=a+bi(a,b∈R), ∵z+=4,z·=8, ∴2a=4,a2+b2=8, 解得a=2,b=±2. ∴z=2±2i. 当z=2+2i时,则=-i. 同理当z=2-2i时,则=i. 故=±i. 答案:B ■(2015江西三县部分高中一模,复数的代数运算,选择题,理3)已知复数z满足z(1+i)=1(其中i为虚数单位),则z=( ) A. B. C. D. 解析:∵z(1+i)=1, ∴z=i. 答案:D ■(2015江西重点中学协作体二模,复数的代数运算,选择题,理2)设i是虚数单位,则=( ) A. B.2 C.3 D. 解析:∵1+i-=1+i+=1+3i, ∴. 答案:D查看更多