混凝土梁梁式桥

混凝土梁梁式桥

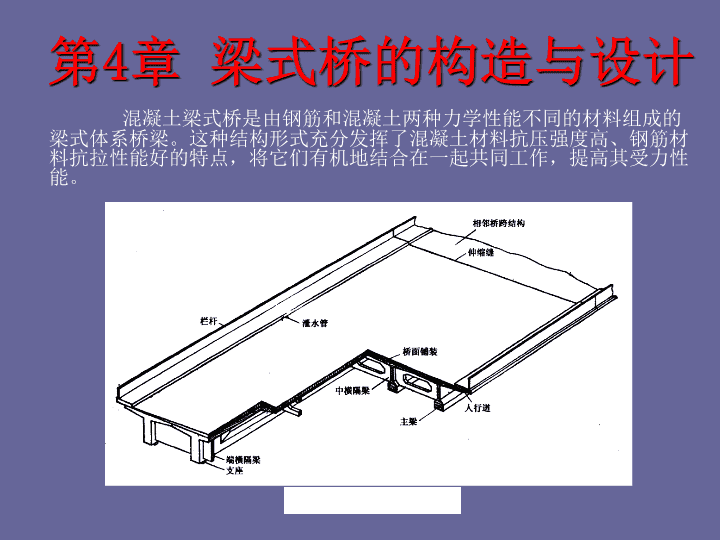
第 4 章 梁式桥的构造与设计 混凝土梁式桥是由钢筋和混凝土两种力学性能不同的材料组成的梁式体系桥梁。这种结构形式充分发挥了混凝土材料抗压强度高、钢筋材料抗拉性能好的特点，将它们有机地结合在一起共同工作，提高其受力性能。 图 4-1 简支梁桥概貌 第 4 章 梁式桥的构造与设计 4.1 混凝土梁式桥的一般特点 易就地取材 耐久性好 可塑可模 整体性好 噪声较小 易开裂 自重大 工期长 R C 梁桥 需要高强钢材和砼 需要专门设备和锚具 施工工艺复杂 P C 梁桥 充分发挥高强材料 跨越能力大 一般不出现裂缝 具有 RC 梁桥的优点 刚度更大 4.2 混凝土梁式桥的主要类型和使用条件 混凝土梁式桥 ( 包括板桥 ) 按不同的划分标准，具有多种不同的结构类型。考虑充分发挥两种不同材料的力学特性，即混凝土受压和钢筋受拉性能，将受拉区混凝土挖空以减轻结构自重，提高其跨越能力为目的，梁式桥的截面形式经历了由板桥、肋板式梁桥到箱形梁桥的演变过程。从改善桥跨结构的整体受力性能，适应桥跨布置的需要，梁式桥分为简支梁 ( 板 ) 桥，悬臂梁 ( 板 ) 桥和连续梁 ( 板 ) 桥。 可分为 板桥 、 肋梁桥 、 箱型梁桥 。 （ 1 ） 板桥 整体式 装配式 组合式 矩形实心板 矮肋板 波形板 实心板 空心板 实心板 板桥 4.2.1 按照截面形式分类 城市高架桥常用异形板式截面 （ 2 ） 肋梁桥 特点 ： 自重较小、梁肋较高、截面抵抗矩 较大、抗弯能力较强 组成 ： 梁肋 （ 腹板 ） 、 翼缘板 、 横隔板 适用跨径 ： RC ： 25m 以下； PC ： 50m 以下 分类 按截面形式分： T 形 、 I 形 、 Π 形 按施工方法分： 整体式 、 装配式 、 组合式 在横截面内形成明显肋形结构的梁桥称为肋板式梁桥，或简称肋梁桥。 （ 3 ） 箱形梁桥 截面呈一个或几个封闭箱形的梁桥。 特点 ： 可承受正、负弯矩；抗弯惯矩、抗扭 刚度都很大；构造较复杂 组成 ： 顶板 、 腹板 、 底板 、 横隔板 分类 按构造形式分： 单箱室 、 多箱室 按施工方法分： 整体式 、 装配式 、 组合式 适用跨径 ： 多用于较大跨径的连续梁桥 箱型梁的构造形式 箱型梁桥的施工方式 （ 1 ） 箱型梁桥的施工方式 （ 2 ） 4.2.1 按照结构受力体系分类 简支梁 悬臂体系 单跨径中小桥梁 ， 多跨已逐渐淘汰 悬臂梁 连续体系 T 构 带铰、带挂梁 连续梁 连续刚构 单悬臂 双悬臂 简支挂梁 刚度大 、 变形小 、 行车 平顺 ， 大跨桥梁的首选 变形大 、 行 车不平顺 ， 现很少采用 4.2.1 按照结构受力体系分类 简支梁 应用最早，使用最广泛的一种桥型 ； 受力简单，设计计算方便 ； 对基础要求低 ； 设计主要受跨中正弯矩控制 ； 经济合理跨径为 20m 以下；预应力结构使全截面参加工作，减轻了结构恒载，增大了跨径，一般在 50m 以下。 4.2.1 按照结构受力体系分类 悬臂梁 悬臂梁利用悬出支点以外的伸臂，使支点产生负弯矩对锚跨跨中正弯矩产生有利的卸载作用。 现较少采用 。 4.2.1 按照结构受力体系分类 连续梁 优点： 变形小、结构刚度大、伸缩缝少、养护简易、抗震能力强、主梁变形挠曲线平缓，行车平顺。 钢筋混凝土连续梁应用较少，而预应力混凝土连续梁的应用却非常广泛 。 钢筋混凝土连续梁跨径一般不超过 25  30 m ，预应力连续梁常用跨径为 40  160 m ，其最大跨径受支座最大吨位限制，目前国内最大跨径尚未超过 165 m( 南京长江二桥北汊桥，其跨径布置为 90m+3  165m+90m) ，如果采用墩上双支座，消去结构在支座区的弯矩高峰，它的跨径可以达到 200 m 。 4.3 板 桥 的设计与构造 板桥的特点 特点 构造简单，制作方便 建筑高度小，外观轻巧 适用范围 简支板桥： RC 板， ≤ 13m ； PC 板， ≤ 25m 连续板桥： RC 板， ≤ 16m ； PC 板， ≤ 30m 4.3 板 桥 的设计与构造 悬臂板桥 从结构受力体系来看，板桥可以分为简支板桥、悬臂板桥和连续板桥 4.3.1 简支板桥的设计和构造 1 、 整体式 简支板桥 截面形式 ： 等厚矩形 、 矮肋式 截面尺寸 ：多采用等截面 板厚与跨径之比一般为： 普通钢筋混凝土 ： 1/12 ～ 1/16 预应力混凝土 ： 1/16 ～ 1/22 板厚通常为 ： 0.2 ～ 0.4m （ 跨径 2 ～ 8m ） 整体式 简支板桥的构造 （ 横 、 纵断面图 ） 2 、 装配式 简支板桥 （ 1 ） 实心矩形板桥 特点 ： 形状简单、施工方便、建筑高度小 尺寸 ： 跨径通常≤ 8m ，板厚 16 ～ 36cm 适用性 ： 小跨径桥梁采用最广泛的形式 装配式 简支板桥 （ 实心 ） 的构造 （ 2 ） 空心矩形板桥 特点 ： 自重较小、运装便易，目前使用较多 适用性 ： RC ： 6 ～ 13m ， PC ： 8 ～ 20m ； 相应跨径的板厚： RC 为 0.4 ～ 0.8m ， PC 为 0.4 ～ 0.9m 充气橡胶芯模 （即 橡胶充气芯 ） 1 、入模 将芯模牵引入钢筋笼 2 、充气 打开阀门，按规格充 气至规定压力 3 、固定 固定芯模，以免上浮 4 、浇筑混凝土 5 、拆模 待砼初凝后，即开阀 放气，将芯模抽出 装配式混凝土空心板桥 — 外观效果图 装配式混凝土空心板桥 — 配筋纵向效果图 1 装配式混凝土空心板桥 — 配筋纵向效果图 2 空 心 矩 形 截 面 配 筋 图 空心矩形 板桥的配筋纵剖面 及钢筋骨架图 先张法预应力空心板 设计 及施工工艺 1 ）确定预应力钢绞线的下料长度，两 端 的 套管应能保 证钢绞线 在其中 自由伸缩 ； 2 ） 预应力钢绞线 张拉控制应力 σ k =0.75 R by = 195 k N； 3 ） 当采用多根钢束同时张拉时，必须在张拉前调正初 应力 ， 初应力约为控制应力的10% ； 4 ） 张拉程序为 0 → 初应力 （ 0.10 σ k ） →1.05 σ k （ 持荷 5min ） →0→ σ k 锚固 ； 5 ） 必须保证橡胶芯 模 的正确位置 ； 6 ）砼 强度达到设计 值 的80%时 ， 方可放松预应力束 ； 7 ） 存放和运输时，支点离梁端不得大于2米。 （ 3 ） 装配式板的横向联结 作用 ： 将装配式板连成整体，共同承受荷载。 常用的联结方法 ： 企口式混凝土铰联结 —— 铰缝内用不低于板体 砼的细骨料砼填实 （ 如图 ） 。该方式能够保证 横向剪力传递，联结效果较好，目前较常用。 钢板联结 —— 预制板 顶面两侧边缘预埋钢 板，安装就位后，用 一块 钢盖板 焊接在相 邻两块预埋钢板上 （ 如图 ）。 钢板联结构造沿 纵向间距通常为 80 ～ 150cm ， 跨中部分较 密 ， 向两端渐疏 。 3 、 装配 — 整体式组合板桥 （ 略 ） 又称 半装配式 。 工艺 ： 将板的 一部分预制 ，做成便于运装 的轻小件，安装完毕后以其作为底 模架， 现浇其余部分 混凝土。 特点 ： 可减轻构件的安装重量，也加强了 板跨结构的整体工作性能（介于 装 配式 和 整体式 之间）。 4.3.2 连续板桥的设计和构造 特点 ： 分为 整体式 和 装配式 两种结构形式 伸缩缝少，行车平稳 由于支座负弯矩的存在，跨径可比简支板桥 增大，或者厚度比同跨径的简支板桥减小 连续板桥属于超静定结构，对于支座沉陷比 较敏感，容易产生附加内力 适用范围 ： 连续板桥一般做成不等跨，边跨与中跨之 比约为 0.7 ～ 0.8 ， 可使各跨跨中弯矩相近 1 、整体式 连续板桥 连续板桥可做成变厚度的，支点截面厚度 较大，约为跨中截面板厚 h 的 1.2 ～ 1.5 倍 。跨中 板厚一般为 h = （ 1/22 ～ 1/30 ） l 。 （ 1 ） 简支 — 连续 接头位置在墩顶 ，并用混凝土浇筑。既保 持了简支板施工简便的优点，又吸取了连续结 构可减小荷载弯矩的长处。 2 、装配式 连续板桥 （ 2 ）悬臂 — 连续 在架设板段时，类似于两边孔为单悬臂、 中孔带挂梁的悬臂体系。接头可以布置在连续 梁恒载弯矩接近于零或较小的位置处。 4.3.3 斜交板桥的受力特点与构造 由于桥位处的地形限制，或由于高等级公路对线型的要求而将桥梁做成斜交 。 斜交板桥的桥轴线与支承线的垂线呈某一夹角，习惯上称此角为斜交角 。 斜板桥虽然有改善线型的优点，但它的受力状态是很复杂的。 1 斜板桥的受力性能 1 ） 荷载有向两支承板之间最短距离方向传递的趋势。 2 ） 各角点受力情况可以用比拟连续梁的工作来描述。 1 斜板桥的受力性能 3 ） 在均布荷载作用下，当桥轴线方向的跨长相同时，斜板桥的最大跨内弯矩比正桥要小，跨内纵向最大弯矩或最大应力的位置，随着斜交角的变化而自中央向钝角方向移动 。 4 ）在上述同样情况下，斜板桥的跨中横向弯矩比正桥的要大，可以认为横向弯矩增大的量，相当于跨径方向弯矩减小的量 。 2 斜板桥的构造特点 《 桥规 》 规定：当整体式斜板桥的斜交角 ( 板的支撑轴线的垂直线与桥纵轴线的夹角 ) 不大于 15 ° 时，可按正交板计算，计算跨径为：当 l/b ≤ 1.3 时，按两支撑轴线的垂直距离的正跨径计算；当 l/b ≥ 1.3 时，按顺桥向纵轴线的斜跨径计算；以上 l 为斜跨径， b 为垂至于桥纵轴线的板宽。装配式铰接斜板桥的预制板块，可按宽为两板边垂直距离，计算跨径按斜跨径的正交板计算。 2 斜板桥的构造特点 斜板钢筋可按照下列规定布置 1 ） 当整体式斜板的斜交角 ( 板的支座轴线的垂直线与桥纵轴线的夹角 ) 不大于 15 ° 时，主钢筋可平行于桥纵轴线方向布置。当整体式斜板斜交角大于 15 ° 时，主钢筋易垂直于板的支座轴线方向布置，此时，在板的自由边下应各设一条不少于三根主钢筋的平行于自由边的钢筋带，并用箍筋箍牢。在钝角部位靠近板顶的上层，应布置垂至于钝角平分线的加强钢筋，在钝角部位靠近板底的下层，应布置平行于钝角平分线加强筋，加强筋直径不宜小于 12 mm ，间距 100~150 mm, 应布置于以钝角两侧 1.0 m~1.5 m 边长的扇形面积内。 2 斜板桥的构造特点 斜板钢筋可按照下列规定布置 2 ） 斜板的分布钢筋宜垂直于主筋方向设置，其直径、间距和数量可按 《 公预规 》 中行车道板的配筋原则配置。在斜板的支座附近宜增设平行于支座轴线的分布钢筋；或将分布钢筋向支座方向呈扇形分布，过渡到平行于支撑轴线。 (3) 预制斜板的主筋可与桥纵轴线平行，其钝角部位加强钢筋及分布钢筋宜按照 (1) 及 (2) 中所述布置。 2 斜板桥的构造特点 1 ） 整体式斜板桥。整体式板桥的斜跨长 l 与垂直于行车方向的桥宽 b 之比一般均小于 1.3 ，根据上面所述斜板主弯矩方向的特点，主钢筋的配置可按图 4-21 所示方式布置。 2) 装配式斜板桥。装配式斜板桥的跨宽比一般均大于 1.3 ，主钢筋沿斜跨径方向配置，分布钢筋在两钝角角点之间的范围内与主钢筋垂直，在靠近支承边附近，其布置方向则与支承边平行。 4.4 装配式简支梁桥的设计和构造 简支梁桥的特点： 静定结构，受力明确，构造简单， 施工方便，中小跨径桥梁中应用广泛。 装配式施工： 构件尺寸易于设计成标准化和系列 化，便于组织大规模预制生产，机械 化、工业化程度高，质量易于控制。 4.4.1 装配式简支 梁桥 的设计 装配式简支梁桥设计主要包括 上部结构 和下部结构形式的选择。 主要包括以下几方面问题： 主梁的横截面型式 横隔梁构造布置方式 主梁块件的划分方式 1 、主梁截面型式选择 有三种： T 形梁桥、 Π 形梁桥 和 箱形梁桥 （ 1 ） T 形梁桥 （ 应用最广泛 ） 优点 ： 构造简单；主梁之间靠横隔梁联结， 整体性好，接头也较方便 缺点 ： 截面形状不稳定，运装复杂；接头在 桥面板跨中，对板的受力不利 适用范围 ： RC ≤16m （ 实际已做到 20m ）； PC ≤50m 开封黄河公路大桥 （ 2 ）箱形梁桥 优点 ： 抗扭能力大；抗弯刚度大，单梁稳定 性好；薄壁箱梁，可减轻自重 缺点 ： 箱梁薄壁构件的预制施工比较复杂 适用范围 ： 一般跨径 ≤ 50m ◆ 对于简支箱梁 ， 应采用 预应力 结构 ， 全截 面参与受力 。 ◆ 不适用于钢砼简支梁桥 ， 因拉区砼不参与 工作 ， 多余的箱梁底板徒然增大了自重 （ 3 ） Π 形梁桥 （ 应用较少 ） 优点 ： 截面稳定， 抗弯刚度大 ， 运装较方便 缺点 ： 制造较复杂 ；两片梁肋较薄，难以做 成大刚度钢骨；跨度较大时， 自重也 较大 适用范围 ： ≤ 13m 的小跨径桥梁 横向联结 ： 块件之间用穿过腹板的螺栓来联 结，以使施工简化 2 、拟定主梁 截面尺寸的一般原则 主梁截面尺寸拟定主要包括：肋板、翼缘板、横隔板尺寸的确定。 （ 1 ）肋板厚度 满足主拉应力强度和抗剪强度需要的前提下，主梁梁肋的厚度，一般都做得较薄，以减轻构件的重量。 《 公预规 》 规定 : “ T 形、 I 形或箱形截面梁的肋板宽度不应小于 140mm ；其上下承托之间的腹板高度，当腹板内设有竖向预应力钢筋时，不应大于腹板宽度的 15 倍。当腹板宽度有变化时，其过渡段长度不宜小于 12 倍腹板宽度差。 高度 ：高跨比多在 1/11 ～ 1/16 之间 宽度 ： 15 ～ 18cm （ 规范规定不小于 14cm ） 2 、拟定主梁 截面尺寸的一般原则 （ 2 ）上翼缘厚度 作用： 满足于桥面板承受的车辆局部荷载要求 截面形式： 端部较薄至根部 ( 梁肋衔接处 ) 加厚 宽度 ：视主梁间距而定 厚度 ：通常为变厚度 ◆ 翼缘悬臂端的厚度应 ≥ 100mm ； ◆ 当使用横向整体现浇联结时 ， 悬臂端厚度 应 ≥ 140mm ； ◆ 与腹板相连处翼缘厚度应 ≥ 梁高的 1/10 。 2 、拟定主梁 截面尺寸的一般原则 （ 3 ）下翼缘尺寸 T 形截面 ，一般下翼缘与肋板等宽，而预应力混凝土 T 形梁截面，下翼缘做成马蹄形（占 T 形梁截面总面积的 10%  20 ％ ） 。 马蹄 总宽度约为肋宽的 2  4 倍，并注意马蹄部分 ( 特别是斜坡区 ) ，管道保护层不宜小于 60mm 下翼缘 高度加 1/2 斜坡区，高度约为梁高的 0.15  0.20 倍，斜坡宜陡于 45  。但下翼缘尺寸也不宜过大、过高。因为下马蹄过大，会降低截面形心，进而使预应力筋的偏心距减小，降低了预加应力的效应 。 2 、拟定主梁 截面尺寸的一般原则 （ 4 ）横隔梁尺寸 作用 ： 将桥面板 连成整体 ，使各主梁共同承 受车辆荷载；对 荷载分配 起主要作用。 应用足够的抗弯刚度。 高度： 一般取主梁高度的 3 ／ 4 左右，横隔梁的肋宽通常采用 120~160mm 。梁肋下部呈马蹄形加宽时，横隔梁延伸至马蹄的加宽处。 中 横隔梁和 端 横隔梁，通常采用相同的尺寸。 3 、块件的划分 装配式混凝土梁桥可以采用多种形式的单元划分，将桥梁承重结构划分为预制单元，然后采用多种联结构造将各预制构件组装成整体。但预制单元的划分方式和联结构造直接影响到结构的整体受力性能，构件的顶制、运输和安装，且各种因素彼此影响、相互矛盾。 3 、块件的划分 （ 1 ）块件划分原则 装配式简支梁桥拼装单元的划分，通常应 遵循的原则是： ①根据施工现场预制、运输和起重条件，确定 拼装单元的尺寸和重量，使其 便于施工 ； ②块件划分应满足受力要求，拼装接头应尽量 设置在 内力较小处 ，接头 数量尽可能少 ； ③块件的种类应尽可能少，其形状和尺寸力求 标准化 ，增强互换性。 （ 2 ）块件划分方式 ① 纵向竖缝划分 （ 应用最为普遍 ） 构造方式：主要承重构件的各根主梁，包括相应行车道板的 H 形梁和 T 形梁，都是整体预制的，接头和接缝仅布置在次要构件 —— 横隔梁和行车道板内 ( 图 4-24b 、 h) ，或直接用螺栓连接 ( 图 4-24a) 。而且结构部分全为预制拼装，不需要现浇混凝土。 优点： 主梁受力可靠，施工方便，现浇数量少 缺点： 构件尺寸和重量往往很大，运装较困难 为减小构件，可缩小桥面板和横隔梁的预制尺寸。 （ 2 ）块件划分方式 ① 纵向竖缝划分 （ 应用最为普遍 ） 如图 4-24d 、 e 所示。在此情况下，构造上要求在预制构件内伸出接头钢筋，待安装就位后通过浇筑部分桥面板和横隔梁混凝土形成桥梁的整体，但要等现浇混凝土达到足够强度后才能进行后续工序的施工。按此种方式构造的桥梁，其横向联结刚度大，桥梁整体受力性能好。同时，可避免由于 T 梁铰缝联结刚度不足，而引起纵向铰缝混凝土的开裂问题。 ② 纵向水平缝划分 （ 组合式结构 ， 如图 ） 构造特点： 采用纵向水平缝将预制梁的梁肋与桥面板分割开来，再借助纵横向的竖缝将板划分成平面呈矩形的预制构件，施工时先架设梁肋，再安装预制板 ( 有时采用微弯板以节省钢筋 ) ，最后在接缝内或连同在板上现浇一部分混凝土使结构连成整体，这样的装配式梁桥通常称为组合式梁桥（ f ， g ， i ） 。 ② 纵向水平缝划分 （ 组合式结构 ， 如图 ） 优点 ： 构件尺寸和重量都较小，制装方便 缺点 ： ◆ 现浇数量多， 整体性 和 稳定性 较差； ◆ 组合梁分阶段受力， 一期恒载 和 二期 恒载 均由梁肋承受，需要增加配筋； ◆ 跨径一般不能做得太大 目前国内外采用的组合式桥梁有 I 形组合 梁桥 （ 适用于 RC 和 PC 简支梁桥 ） 和 箱 （ 槽 ） 形 组合梁桥 （ 仅适用于 PC 梁桥 ） 。 纵向竖缝划分 （ 组合梁 ） ③ 纵 、 横向竖缝划分 欲使装配式梁的预制块件进一步减小尺寸 和减轻重量，可将用 纵向竖缝划分 的主梁再通 过 横向竖缝划分 成较小的梁段。 横向分段预制的装配式梁也称 串连梁 ，块 件尺寸和重量小 ，可工业化成批预制 ，逐段拼 装 （ 在梁段接触面处涂有 ≤ 1mm 厚的环氧树脂 ） 。 横向分段的简支梁应用很少，主要用于连 续梁、连续刚构的 悬臂拼装施工 。 4.4.2 装配式钢砼简支 梁桥 构造 装配式钢筋混凝土简支 T 梁桥在工程中应用普遍 4.4.2 装配式钢砼简支 梁桥 构造 1 、构造布置 （ 1 ）主梁布置 关键点 ： 主梁的间距、选定片数 影响到 ： 钢筋、混凝土的材料用量，构件的吊 装重量，翼板的刚度等 一般说来，适当加大主梁间距，减少片 数，钢筋砼的用量会少些，比较经济；但桥面 板跨径增大，刚度减小。目前 常用的主梁间距 为 1.6 ～ 2.2m 。 （ 2 ）横隔梁布置 作用 ： 横向联结，加强桥梁的整体性，增加 翼缘刚度，分布荷载 缺点 ： 与主梁一起预制，横隔梁与主梁交界处模板复杂化，增加了脱模的难度。横隔梁做成上宽下窄的形式。 布置要点 ： ◆ 端横隔梁 必须设置 （ 可增加构件的稳定 性和全桥结构的整体性 ） ◆ 中横隔梁 一般 4 ～ 6m 设置一道 （ 荷载横 向分布比较均匀 ， 且可以减轻翼板接缝处 的纵向开裂现象 ） 4.4.2 装配式钢砼简支 梁桥 构造 2 、主梁钢筋构造 （ 1 ）一般构造 T 主梁钢筋主要有纵向主钢筋、架立钢筋、斜钢筋、箍筋和分布钢筋等几种 。 主梁受力： 简支梁承受正弯矩作用且截面下缘受拉，故抵抗拉力的主钢筋应设置在梁肋的下缘。随着弯矩向支点处减小，主钢筋可在跨间适当位置处切断或弯起。 2 、主梁钢筋构造 （ 1 ）一般构造 《 公桥规 》 规定： 钢筋混凝土梁内纵向受拉钢筋不宜在受拉区截断； 2 、主梁钢筋构造 （ 1 ）一般构造 《 公桥规 》 规定： 钢筋混凝土梁的支点处，应至少有 2 根且不少于总数的 1/5 的下层受拉主钢筋通过，两外侧钢筋，应延伸出端支点以外，并弯成直角，顺梁高延伸至顶部，与顶层纵向架立钢筋相连。 2 、主梁钢筋构造 （ 1 ）一般构造 《 公桥规 》 规定： 对于各种受力钢筋，如通过计算和作图允许将其在梁内切断，则被切断的钢筋应当比理论切断点再放长一个规定的锚固长度，以保证该钢筋从理论切断点起能充分受力。 2 、主梁钢筋构造 （ 1 ）一般构造 箍筋和弯起主筋的布置 箍筋 直径：不小于 1/4 主筋直径； 配筋率：不应小于 0.18% 间距： 不大于梁高的 1 ／ 2 且不大于 400mm ； 所箍钢筋为按受力需要的纵向受压钢筋时，不应大于所箍钢筋直径的 1.5 倍，且不应大于 400mm ； 在箍筋绑扎搭接接头范围内的箍筋间距，当绑扎钢筋受拉时，不应大于主钢筋直径的 5 倍，且不大于 100mm ；当搭接钢筋受拉时，不应大于主钢筋直径的 10 倍，且不大于 200 mm ； 支座中心向跨径方向长度相当于不小于一倍梁高范围内，箍筋间距不宜大于 100 mm ； 近梁端第一根箍筋、 靠近交接面的一根箍筋 。 2 、主梁钢筋构造 （ 1 ）一般构造 箍筋和弯起主筋的布置 弯起主筋 ： 《 桥规 》 中对弯起钢筋的弯起角度、弯起点等均做了规定。 2 、主梁钢筋构造 （ 1 ）一般构造 分布钢筋的布置 为了防止梁肋侧面因混凝土收缩等原因而导致混凝土裂缝，因此需要设置纵向防裂分布钢筋 。 《 公桥规 》 中对 T 形 I 形箱形截面的分布钢筋均做了规定。 2 、主梁钢筋构造 （ 1 ）一般构造 架立钢筋的布置 架立钢筋 布置在梁肋的上缘，主要起固定箍筋和斜筋并使梁内全部钢筋形成立体或平面骨架的作用。 保护层厚度的规定 作用： 为了防止钢筋受到大气影响而锈蚀，并保证钢筋与混凝土之间的粘着力充分发挥作用，钢筋到混凝土边缘需要设置保护层。 保护层厚度太小，就不能起到以上作用，太大则混凝土表层因距钢筋太远容易破坏，且减小了钢筋混凝土截面的有效高度，受力情况也不好。 2 、主梁钢筋构造 （ 1 ）一般构造 保护层厚度的规定 《 公桥规 》 规定 最小保护层厚度不应小于钢筋的公称直径且应符合规范中的相关规定； 受弯构件的钢筋净距应考虑浇筑混凝土时，振捣器可以顺利插入。各主钢筋间横向净距和层与层之间的竖向净距，当钢筋为三层及以下时，不应小于 30mm ，并不小于钢筋直径；当钢筋为三层以上时，不应小于 40mm ，并不小于钢筋直径的 1.25 倍。 2 、主梁钢筋构造 （ 1 ）一般构造 装配式 T 梁结构 问题 钢筋数量多，如按钢筋最小净距要求排列有困难 解决方法： 将钢筋叠置，并与斜筋、架立钢筋一起焊接成钢筋骨架 ； 焊接钢筋骨架整体性好，能保证钢筋与混凝土共同工作，其钢筋重心位置较低，梁肋混凝土体积也较小，此外可避免大量就地绑扎工作 （常用形式） 问题 ：焊接钢筋骨架的主筋与混凝土的粘结面积较小，一般说来抗裂性能稍差 解决方法 在实践中采用螺纹形或竹节形钢筋，并选用较小直径的钢筋，有条件时还可将箍筋与主筋接触处点焊固结，以增大其粘结强度，从而改善其抗裂性能 2 、主梁钢筋构造 （ 1 ）一般构造 装配式 T 梁结构 钢筋混凝土梁采用焊接钢筋时，可用侧面焊缝使之形成骨架 ( 图 4-34) 。侧面焊缝设在弯起钢筋的弯折点处，并在中间直线部分适当设置短焊缝。 2 、主梁钢筋构造 （ 1 ）一般构造 装配式 T 梁结构 T 形梁翼缘板内的受力钢筋沿横向布置在板的上缘，以承受悬臂负弯矩。同时，在顺主梁跨径方向还应设置一定数量的分布钢筋 。 《 公预规 》 对行车道板和人行道板内的主钢筋及分布钢筋的直径、间距均做了规定。 2 、主梁钢筋构造 （ 1 ）一般构造 装配式 T 梁结构 (1) T 梁翼缘板 ( 行车道板 ) 内主钢筋直径不应小于 10mm 。人行道板内的主钢筋直径不应小于 8mm 。在简支板跨中和连续板支点处，板内主钢筋直径间距不应大于 200mm 。 (2) 行车道板内应设置垂至于主钢筋的分布钢筋。分布钢筋设在主钢筋的内侧，其直径应不小于 8mm ，间距不应大于 200mm ，截面面积不宜小于板的截面面积的 0.1% 。在主钢筋的弯折处，应布置分布钢筋。人行道板内分布钢筋直径不应小于 6mm ，其间距不应大于 200mm 。 （ 2 ）主梁钢筋构造实例 （ 2 ）主梁钢筋构造实例 （ 3 ）装配式主梁的联结构造 装配式梁桥中，借助横隔梁的接头使主 梁 联结成整体 。接头要有 足够的强度 以保证结 构整体性，并使在运营过程中不致因 反复荷载 和 冲击作用 而发生松动。 横隔梁接头的连接方式常见的有三种：钢板连接接头，螺栓连接接头和现浇湿接头。 （ 3 ）装配式主梁的联结构造 钢板连接接头 在横隔梁靠近下部边缘的两侧和顶部翼板内设置预埋的焊接钢板 A 和 B ( 图 4-37) ，焊接钢板预先与横隔梁的受力钢筋焊在一起做成安装骨架。 （ 3 ）装配式主梁的联结构造 钢板连接接头 T 形梁安装就位后，在横隔梁的预埋钢板上再加焊盖接钢板使各片主梁联结成整体 ( 图 4-38) 。 相邻横隔梁之间的缝隙需用水泥砂浆填满，所有外露钢板也要用水泥灰浆封盖，以防连接钢板锈蚀。 这种接头强度可靠，焊接后立即就能承受荷载，但现场要有焊接设备，而且有时需要在桥下进行仰焊，施工较困难。 端横隔梁的焊接钢板接头外侧 ( 近墩台一侧 ) 不易施焊，故焊接接头只设于内侧。 （ 3 ）装配式主梁的联结构造 螺栓连接接头 基本上与焊接钢板接头相同，不同之处是盖接钢板不用电焊，而是用螺栓与预埋钢板连接，为此钢板上要预留螺栓孔。这种接头由于不用特殊机具而有拼装迅速的优点，但在运营过程中螺栓易于松动 ( 图 4-39) 。 （ 3 ）装配式主梁的联结构造 螺栓连接接头 通过预制横隔梁端部伸出的预留钢筋之间进行搭接，然后现浇混凝土的方法实现横隔梁之间的连接。 做法是：横隔梁在预制时在接缝处伸出钢筋扣环 A ，安装时在相邻构件的扣环两侧再安上腰圆形的接头扣环 B ，在形成的圆环内插入短分布筋后现浇混凝土封闭接缝，接缝宽度约为 0.20 ～ 0.50m 。 接头强度可靠整体性好，在工地不需要特殊机具。但现浇混凝土数量较多，接头施工后也不能立即承受荷载。此种连接构造常用于主梁间距较大而需要缩减预制构件尺寸和重量的场合。 RC 简支梁桥 当跨径超过 20m 时，构件尺寸和材料用量 均显著增大，而且混凝土开裂现象严重，影响 结构耐久性。因此多采用 PC 简支梁桥 。 PC 简支梁桥 横截面类型和构件的划分方式，均与 RC 梁桥相同。最常采用的是 纵向竖缝划分 的 T 形 梁。此外，还可做成横向也分段的 串连梁 。 4.4.3 装配式预应力混凝土 简支 梁桥 1 、构造布置 梁肋： 下部增设 马蹄 以便布设预应力筋。 梁端 至少一 倍梁高的距离范 围内 ， 腹板与马 蹄同宽 （ 如图 ） ， 以配合预应力筋 弯起 、 两端布置 锚头以及安放张 拉千斤顶 。 2 、截面尺寸 （ 1 ）高跨比 高跨比一般取 1/15 ～ 1/25 。 允许情况下，采用较大的梁高可节省较多 的预应力筋，此时可取 1/16 ～ 1/18 。 （ 2 ）翼板 厚度确定原则与 RC 梁相同。 （ 3 ）肋板 在 PC 梁内，肋宽一般由 构造 和 施工要求 来 确定。实践中，肋宽通常采用 0.14 ～ 0.16m 。 （ 4 ）马蹄 马蹄的 形状 和 尺寸 要视预应力筋数量和排 列而定，还要考虑施工方便和弯起筋的要求。 马蹄面积 不宜少于全截面的 10 ～ 20% （ 防 止产生纵向裂缝 ） 。此外，具体尺寸建议如下： ①马蹄宽度约为肋宽的 2 ～ 4 倍，马蹄部分（ 特 别是斜坡区 ）的管道保护层厚度宜 ≥ 6cm ； ② 马蹄全宽部分高度 + 1/2 斜坡区 的高度约为 （ 0.15 ～ 0.2 ） h ，斜坡宜＞ 45 度。 4.4.3.2 、配筋设计与构造 预应力混凝土简支梁内的配筋，除纵向预应力筋外，尚有架立钢筋、箍筋、水平分布钢筋、承受局部应力的锚下加强钢筋和其他构造钢筋等。 ①各种配筋的作用和构造特点； ②预应力混凝土构件的设计方法； ③预应力钢束布置方式； ④预应力钢束的锚固方法及锚下加强钢筋的配置。 1 预应力钢筋设计 （ 1 ）截面效率指标 在截面尺寸的拟定与预应力钢束的配置之间合理设计的技术指标。 截面效率指标体现了在截面尺寸及预应力钢筋确定的条件下，截面设计与配筋设计的优化设计方法。 预应力混凝土简支梁在预加应力阶段和使用阶段，截面上下缘不出现拉应力为技术标准，探讨截面的最优化设计与预应力钢筋的合理布置方法之间的关系。 1 预应力钢筋设计 （ 1 ）截面效率指标 首先，为了合理设计预应力混凝土梁的截面尺寸，下面按简支梁在预加力阶段和运营阶段上、下缘拉应力为零的前提下，分析其截面的受力特点。 1 预应力钢筋设计 （ 1 ）截面效率指标 在预加力阶段，假定施加偏心预加力为 Ny ，偏心距为 e ，截面由支点向跨中的变化过程中，梁内的自重弯矩逐渐增加。从应力图形来分析，预加力与自重形成的合力 N 的作用点逐渐上移 。在跨中截面预加力和自重弯矩 Mgl 的共同作用下，合力 N 移动了距离 e ’ ，而达到了截面的下核点，截面上缘就达到零应力状态。 1 预应力钢筋设计 （ 1 ）截面效率指标 在运营阶段，如果计及预加力损失 Δ Ny 后截面内合力为 N ’ y = Ny -Δ Ny ，则在后期恒载 ( 桥面铺装、人行道、栏杆 ) 弯矩 Mg2 和活载弯矩 Mp ，作用下，合力 N ’ y 将从下核点移至上核点 , 即移动了 K = ku + k0 的距离，此时截面下缘的应力刚好为零。 1 预应力钢筋设计 （ 1 ）截面效率指标 对以上两个受力阶段可写出内力平衡式： 从式 (4-1) 可以看出，偏距 e ’ 实际上起了抵消主梁自重的作用，而且 e ’ 大了，可以减小 Ny ，从而节约了预应力筋的数量。因此在截面设计中应使截面的形心要高，这样才能加大偏距 e ’ 。这也说明了当跨度较大、自重较大时一般应增大梁距采用较宽翼缘板的原因。 1 预应力钢筋设计 （ 1 ）截面效率指标 对以上两个受力阶段可写出内力平衡式： 从式 (4-2) 可以看出，截面核心距的大小体现了运营阶段承受荷载的能力，而且核心距 K 愈大预应力筋就愈节省。 在此假设截面效率指标为核心距与梁高的比值 1 预应力钢筋设计 （ 1 ）截面效率指标 在此假设截面效率指标为核心距与梁高的比值 不同截面形式的效率指标有一定的取值范围， ρ 值较大的截面较为经济，通常希望 ρ 值在 0.45 ～ 0.5 以上。在具体设计中，还要视 g 1 ／ ( g 2+ p ) 的荷载比值和梁高是否受限制来考虑。 1 预应力钢筋设计 （ 2 ）截面细部尺寸 预应力混凝土简支梁桥的主梁高度按截面形式、主梁片数及建筑高度要求，可在较大范围内变化。 从经济观点出发，当桥梁建筑高度不受限制时，采用较大的梁高显然是有利的，因为加高腹板使混凝土量增加不多，但节省预应力筋数量较多。故对于一般中等跨径的预应力混凝土 T 梁，高跨比可取 1/16~1/18 左右。 T 梁翼板的厚度对于中小跨径按钢筋混凝土梁桥同样的原则来确定。为了减小翼板和梁肋连接处的局部应力集中和便于脱模，在该处一般还设置折线形承托或圆角。在预应力混凝土梁内，由于混凝土所受预压应力和预应力筋弯起能抵消荷载剪力的作用，肋中的主拉应力较小，因而肋宽一般都由构造和施工要求决定。从截面效率指标 ρ 来分析，肋板愈薄， ρ 值也愈大。实践中通常采用 0.14~0.16 m 。 1 预应力钢筋设计 （ 3 ）预应力钢束索界 后张法预应力混凝土简支梁中预应力筋曲线布置的范围，以保证截面在各个受力阶段不出现拉应力。 以张拉和运营阶段梁的上、下缘允许出现不大于规定拉应力值的部分预应力截面为例。 由规定的拉应力值就可确定截面的特征点 —— 限心点 Co 和 Cu ，显然限心距 C0Cu 将大于核心距 K 。 1 预应力钢筋设计 （ 3 ）预应力钢束索界 按照对于 “ 截面效率指标 ” 同样的分析方法可知，从下限心点 Cu 向下量取 Mgl / Ny 所得的曲线为索界下限，从上限点 C 。 向下量取∑ M ／ N ’ y ，所得的曲线为索界上限 ( 图 4-44) 。这样，只要所布置的预应力筋重心位于此界限以内，就能保证梁任何截面在各个受力阶段上下缘应力都不超过规定值。同理，也可以绘出两个受力阶段受压区不超过允许值的相应索界线。显然，在实际布置时还要满足混凝土规定保护层的要求。 1 预应力钢筋设计 （ 3 ）预应力钢束索界 从图中可见，由于简支梁弯矩向着梁端逐渐减小，故索界的上下限也逐渐上移，至支点处弯矩为零时，索界就是 C0 和 Cu 点。这就是为什么在预应力钢筋布置时，必须将大部分预应力筋向梁端逐渐弯起的重要原因之一。 1 预应力钢筋设计 （ 4 ）剪余剪力图 在任意截面内，当预应力筋的预加力 N ，具有倾角 α 时，对于混凝土截面必然产生与荷载剪力相反的竖向分力 ( 或称预剪力 ) Qy = Nysina ，它随 α 角的增大而增大，起弯的力筋愈多，朝着支点方向所累计的 Qy 值也愈大。 1 预应力钢筋设计 （ 4 ）剪余剪力图 弯起的预应力筋显著抵消了梁内的荷载剪力，这样就大大减小了预应力混凝土梁内的剪应力，并进一步降低了腹板所承受的主拉应力。这也是要将预应力筋弯起的另一重要原因。 1 预应力钢筋设计 （ 4 ）剪余剪力图 在实际设计中，鉴于梁在跨中区段弯矩变化平缓，荷载剪力也不大，故通常在三分点到四分点之间开始将预应力筋弯起。 预应力筋在跨中横截面内的布置，应在保证梁底保护层和位于索界内的前提下，尽量使其重心靠下，以增大预加力的偏心距，节省高强钢材。同时应使预应力筋在满足构造要求的同时，尽量相互靠拢，以减小下马蹄的尺寸。此外还应将适当数量的预应力筋布置在腹板中线处，以便于起弯。 预应力筋起弯的曲线形状可以采用 圆弧 形 、 抛物线 或 悬链线 三种。 圆弧线 施工放样方便，弯起角度较大，可得 到 较大的预剪力 ，故通常在梁中部保持一段 水平直线后按圆弧弯起。 悬链线 预应力筋可利用其 自重下垂 达到规定 线形，定位方便，但在端部弯起角度较小。 预应力筋弯起的 曲率半径 ，当采用钢丝束、 钢绞线配筋时，一般不小于 4m 。 3 、配筋特点 2 纵向预应力筋布置 预应力混凝土结构中预加应力的作用是对混凝土构件预先施加与使用荷载方向相反的荷载 , 用以抵消部分或全部荷载效应的一种方法。预应力混凝土简支梁设计中，预应力钢筋布置在满足束界界限要求的前提下，预应力钢筋的布置 ( 特别是跨中截面 ) 一般应尽量靠近截面的下缘布置，以抵消荷载在截面下缘产生的拉应力。 3 、配筋特点 2 纵向预应力筋布置 预应力主筋布置可分为 直线形布置 和 曲线 形布置 两大类，跨中主筋均靠近梁下缘布置。 ① 直线形布置 构造简单，多用于 先张法 小跨度梁。缺点 是张拉负弯矩可能引起梁顶开裂。 对较大跨度的 后张法 梁，可将直线形预应 力筋在横隔梁处平缓弯出，以便张拉锚固。 ② 曲线形布置 目前预应力混凝土简支梁上采用最广的布 筋方式是 图 b （ 预应力筋全部弯至梁端锚固 ） 和 图 c （ 部分预应力筋弯出梁顶 ） 两种。 3 纵向预应力筋的锚固体系 先张法 ： 钢丝或钢筋靠砼的握裹力锚固在梁体内 后张法 ： 钢丝或钢筋通过锚具锚固于梁端或梁顶 ① 先张法的锚固 钢丝切断后，外端 回缩，钢丝内应力通过 与砼之间 摩阻和粘结 传 至砼。至传递长度 l c 处 握裹力为零，砼承受全 部预应力。此时传力区 会出现 劈裂力 （ 如图 ） 。 传递长度 l c 的大小取决于梁端 砼的品质 、 钢丝直径 和 钢丝表面形状 等。 ◆ 直径 d =3 ～ 5mm 的冷拔低碳钢丝 l c ≈ （ 80 ～ 90 ） d ◆ 直径 d =7.5 ～ 15mm 的钢绞线 ， l c 可取 （ 70 ～ 85 ） d 为使预应力筋可靠的锚固，宜将构件的 端截 面加宽 ； 锚固区内应配置足够的 围包纵向预应力筋 的 封闭式箍筋或螺旋筋。 为 减小钢丝回缩量 和 传递长度 ，可将钢丝端 部轧成波浪形或做成钢丝 “ 锚结 ” 来加强锚固 作用。 ② 后张法的锚固 ◆ 锚具底部对砼有很大压力，且 应力较集中 ； ◆ 锚具附近很大 压应力 和较大 拉应力 （ 劈裂力 ） ； ◆ 为防止锚具附近砼开裂，必须配置足够的钢 筋予以 加强 。 梁端锚固区 （ ≈ 梁高长度内 ） 的配筋构造： ◆ 加强钢筋网的网格为 10 × 10cm ； ◆ 锚具下设置厚度不小于 16mm 的 钢垫板 与 ф 8 的 螺旋筋 ，以提高砼的抗裂性。 ◆ 也可以采用带有预埋锚具的 预制钢筋混凝土 端板 来锚固预应力筋。 ◆ 预埋式锚具 也常常用于预应力筋弯出梁顶的 情况。 ◆ 锚具在梁端的布置应遵循 分散 、 均匀 的原 则，尽量减小局部应力集中 ◆ 锚具应在梁端对称于竖轴布置，锚具之间应 有足够的净距，安装张拉设备，方便施工。 后张法预应力筋锚固构造 梁端预埋钢砼端板 （ 后张法 ） 4 其他钢筋的布置 ◆ PC 梁应按构造要求布置 箍筋 、 架立筋 和 纵向 水平分布筋 等 （ 主拉应力较小 ， 可 不设斜筋 ） ； ◆ 预应力筋比较集中的 下马蹄 内，必须设置闭 合式或螺旋形的加强箍筋 （ 间距 ≤ 20cm ） ； ◆ 制孔管的直径应比预应力筋直径大 10mm （ 采 用铁皮套管时应大 20mm ） ； ◆ 管道间最小净距主要由浇筑砼的要求而定， 在有良好振捣工艺 （ 如同时采用 底振 和 侧振 ） 时，最小净距 ≥ 4cm 。 在 PC 梁中，为弥补局部梁段强度不足，或 为更好的 分布裂缝 和提高梁的 韧性 ，可将无预 应力筋与预应力筋协调配置。 如图 （ a ）， 当梁中预应力筋在两端不便弯 起时 ， 为防止张拉阶段 梁端顶部 可能开裂而布 置受拉钢筋 。 如图（ b ），梁重比恒载和活载小得多，在 预加力阶段跨中上翼缘可能会开裂而破坏： ◆ 可在 跨中部分的顶部 加设普通纵向受力筋 。 ◆ 这种钢筋还能在运营阶段加强混凝土的抗压 能力 ， 在破坏阶段则可提高梁的安全度 。 如图 （ c ）， 在 跨中部分下翼缘 设置钢筋 。 如图 （ d ）， 下翼缘 设置通长纵向钢筋 。 第 5 章 简支梁 桥 的计算 5.1 概述 1 、 桥梁工程计算的内容 内力计算 —— 《 结构力学 》《 桥梁工 程 》《 基础工程 》 等 截面验算 —— 《 混凝土结构原理 》 等 变形验算 —— 《 材料力学 》《 结构力 学 》《 桥梁工程 》 等 2 、简支梁桥计算的构件 上部结构 行车道板 ：直接承受车辆荷载 主梁 ：主要承重构件 横隔梁 ：增强横向刚度和结构整体性， 同时起到分布荷载的作用 支座 下部结构 —— 桥墩 、 桥台 计算顺序 ： 先上部 （ 先桥面板后主梁 ） 后 下部 。 3 、简支梁桥计算流程图 5.2 行车道板的计算 1 、行车道板的类型 混凝土肋梁桥的 行车道板是直接承受车辆轮压的钢筋混凝土板， 既保证了桥梁的 整体作用 ，又将 荷载传递 给主梁。 5.2 行车道板的计算 1 、行车道板的类型 结构形式 ： 在简单梁格和复杂梁格体系中，行车道板实际上是周边支承的板 。 受力特点 ： 在矩形的四边支承板上当板中央作用一竖向荷载 P 时，虽然荷载 P 要向相互垂直的两对支承边传递，但由于板沿 la 和 lb 跨径的相对刚度不同，因此传递的荷载也不相等。对于四周简支的板， 当长短边之比 l a / l b ≥ 2 时，荷载绝大 部分沿短跨方向传递，而沿长跨方 向传递的荷载不足 6% （ 均布 ） 。 梁格构造和桥面板支承方式 双向板工作原理模型 为此，可将四边支承的板分为两类： 常用的行车道板，按受力可分为三类： 单向板 （ 美国规范 ： l a / l b ≥1.5 时按单向板计算 ） 悬臂板 （ 主梁的翼板间采用 钢板联结 ） 铰接悬臂板 （ 主梁的翼板间采用 铰接缝联结 ） 单向板 l a / l b ≥ 2 ， 荷载主要由短跨承受，在长跨方向只需 适当配置分布钢筋即可（ 在桥面板中较为常用 ） 双向板 l a / l b ＜ 2 ， 需按两个方向的内力分别配置受力钢 筋，用钢量大，构造复杂（ 桥面板中较少采用 ） 桥面板的受力分析 5.2.2 车轮荷载在板上的分布 ① 基本假定 ◆ 轮压经桥面铺装扩散分布于行车道板， 在计算中 将轮压作为分布荷载 来处理； ◆ 为计算方便，将较为复杂的 轮压分布形 态近似当作矩形 ； ◆ 据试验研究，铺装层对 轮压近似呈 45 ° 扩散 。 a 2 —— 沿行车方向车轮着地长度； （ 公路 ： 0.2m ； 城市 ： 0.25m ） b 2 —— 垂直于行车方向车轮的着地长度； （ 公路 ： 前轮 0.3m ； 中 、 后轮 ： 0.6m ） （ 城市 ： 前轮 0.25m ； 中 、 后轮 ： 0.6m ） H —— 桥面铺装层的平均厚度。 ② 车轮压力面计算 作用于混凝土桥面板顶面的矩形 压力面边 长 为 （ 如图 ） ： 沿桥纵向 ： a 1 = a 2 +2 H 沿桥横向 ： b 1 = b 2 +2 H P —— 加重车后轮轴重 ③ 局部分布荷载计算 沿桥纵向 ： a 1 = a 2 +2 H 沿桥横向 ： b 1 = b 2 +2 H 当加重车的后轮作用于桥面板上时，作用于板面上的局部分布荷载 1.8 m 轮距 15×2.5 m 车辆外形长 × 宽 0.6×0.2 m 中后轮宽 × 长 0.3×0.2 m 前轮宽 × 长 3+1.4+7+1.4 m 轴距 技术指标 单位 项目 2×140 kN 后轴重力标准值 2×120 kN 中轴重力标准值 30 kN 前轴重力标准值 550 kN 车辆重力标准值 技术指标 单位 项目 车辆荷载主要技术指标 5.2.3 板的有效工作宽度 （ 荷载有效分布宽度 ） 行车道板不仅直接承压部分 （ 例如宽度为 a 1 ） 的板带参加工作，与其相邻的部分板带也会 分担一部分荷载而共同参与工作。 因此，桥面板计算中，需要确定板的 有效 工作宽度 （共同 参与工作的板的宽度范围）。 ◆ 两边固结的板有效工作宽度比简支的 小 30% ～ 40% ◆ 全跨满布条形荷载有效工作宽度比局部分布荷载小 ◆ 荷载越靠近支承边 ， 有效工作宽度也越小 ① 单向板 已知跨径为 l 的 单向板 ，车轮荷载以 a 1 × b 1 的分布面积作用在行车道板上，则 ◆ 板在计算跨径 x 方向 产生挠曲变形 ω x ，同 时也在 y 方向 产生挠曲变形 ω y （如图） ； ◆ 直接承压的宽为 a 1 的板条受力最大，其 邻近 板也参与工作 ， 共同承受轮载产生的弯矩 ； ◆ 离荷载越远的板条承受的弯矩越小。 简便起见，用 宽为 a ， 高为 m x max 的矩形面 积代替弯矩图曲线面积来计算轮载总弯矩，即 等效弯矩图 的总宽度为 ◆ a 即为 荷载有效工作宽度 或 板的有效分布宽度 ； ◆ 每延米板条荷载强度为 ： p = P / (2 ab 1 ) 轮载产生的 跨中总弯矩 荷载中心处最 大单宽弯矩值 《 公预规 》 （ JTG D62-2004 ） 对单向板 的 荷载有效分布宽度 a 规定如下： 单向板的荷载有效分布宽度 1 ）车轮位于板的跨中 多个车轮在板的跨中时 （ 如图 b ， 当各单个车轮按上 式计算的荷载分布宽度发生重叠时 ， 按下式计算 ） ： 单个车轮在板的跨中时 （ 如图 a ） ： 2 ）车轮位于板的支承处 （ 如图 c ） 3 ）车轮位于板的支承处附近，距离支点 x 时 式中： l —— 板的计算跨径 ； d —— 多个车轮时外轮之间的中距 ； t —— 板的厚度 ； x —— 荷载作用点至支承边缘的距离。 ② 悬臂板 由理论分析，当板端作用集中力 P 时 （ 如 图 b ） ， 板条的最大负弯矩为 m x max = − 0.465 P , 而荷载引起的总弯矩为 M 0 = − Pl 0 。 因此，按最 大负弯矩换算的 有效工作宽度 为 （ 如图 a ） ： 因此，可以近似的认为 荷载按 45 ° 角向 悬臂板支承边分布。 悬臂板规定的有效宽度为 （ 如图 ） ： 式中： b ' —— 承重板上的荷载压力面外缘至悬臂板 根部的距离 ， b ' ≤2.5m 。 对分布荷载 靠近板边的最不利情况 ， 有 ： a = a 1 +2 l 0 【 注 】 当 b ' > 2.5m 时，悬臂根部的负弯矩应扩大为 1.15 ～ 1.30 倍。 此外，车轮荷载作用点下方 还会出现正弯矩，尚应考虑正弯矩配筋。 ③ 履带车不计有效宽度 5.2.4 行车道板的内力计算 式中： n —— 桥面板有效分布宽度范围内的车轮数 ； P —— 汽车轴重。 实体矩形截面的行车道板通常由 弯矩控制 设计 ， 习惯以 每米宽 板条来进行计算 。 计算参数 作用于 每米宽 板条上的荷载集度为： （ 1 ）多跨连续单向板的内力 由于板与主梁连结成整体，板上的荷载引 起主梁变形，而这种变形又影响到板的内力。 ◆ 主梁抗扭刚度极大 ， 板接近于 固端梁 （ 图 a ） ； ◆ 主梁抗扭刚度极小 ， 板在支承处接近自由转动的铰支座 ， 则板的受力就如 多跨连续梁 体系 （ 图 c ） ； ◆ 行车道板与主梁之间实际上是 弹性固结 （ 图 b ） 。 由于行车道板受力较复杂，因此通常采用 简化近似方法 —— 按 简支板计算 。 ① 跨中最大弯矩 先求相同跨径的 1m 简支板跨中弯矩 M 0 并修正。 弯矩修正系数 可视板厚 t 与主梁肋高 h 的比值选用 ： 当 t / h< 1/4 时 （ 主梁抗扭能力较大 ） ： 跨中弯矩 M C = + 0.5 M 0 支点弯矩 M S = − 0.7 M 0 当 t / h ≥ 1/4 时 （ 主梁抗扭能力较小 ） ： 跨中弯矩 M C = + 0.7 M 0 支点弯矩 M S = − 0.7 M 0 M 0 包括两部分： M 0g 和 M 0p 。 内力组合 （ 承载力极限状态 ， 下同 ） ： M 0g —— 1m 宽简支板条恒载引起的跨中自重弯矩： M 0p —— 1m 宽简支板条活荷引起的跨中自重弯矩： 单向板内力计算图示 ② 支点剪力 计算单向板剪力时按简支板的图示进行。 ② 支点剪力 计算单向板剪力时按简支板的图示进行。 对于跨内只有一个车轮荷载的情况 ， 宽度 为 1m 的简支板支点 活载剪力 Q SP 的计算公式为 ： 恒载剪力 Q Sg 则为 ： q 、 q ' —— 对应于有效宽度 a 、 a ' 处的荷载集度 ： A 1 —— 矩形部分合力 ： A 2 —— 三角形部分合力 ： 若行车道板跨径内不止一个车轮，尚需计 其他车轮的影响。 y 1 、 y 2 —— 对应于 A 1 、 A 2 的支点剪力 影响线竖标值 。 （ 2 ）铰接悬臂板的内力 沿纵缝按铰接方式连接的 铰接悬臂板 ， 最 大弯矩在悬臂根部 . ① 铰接悬臂板的内力影响线 对于相邻翼缘板沿板边互相做成铰接的桥面板，按铰接悬臂板计算 ; 常截面的板、变截面板； 如为变截面板，则影响线坐标值应另行确定。 ② 铰接 悬臂板最大弯矩 a. 利用影响线进行计算 计算板根部的活载弯矩 Msp 时，按弯矩影响线进行 最不利布载 ，将一个轮压面宽度 b 1 的车轮荷载放在 弯矩影响线的峰值附近 ，使轮压下的影响线 面积 为 最大 ，板跨较大时，两旁的车轮压力面可能有 c 宽度的部分荷载进入板跨内，则弯矩为： pi —— 根据板的有效工作宽度所计算的车轮分布荷载集度 ωi—— pi 对应下的弯矩影响线面积； ② 铰接 悬臂板最大弯矩 作用在计算点 A 处 作用在板跨中部 计算活载弯矩时将 活载对称布置于铰接处 b. 实用简化计算 用影响线计算，需要找最不利位置，求荷载下的影响线面积比较繁琐。 汽车荷载为非对称荷载，但由铰剪力影响线可见，进入板跨内 c 长度的荷载产生的铰剪力很小，故可忽略铰剪力的影响。因此，实用计算中可以按自由悬臂板来计算板根部的活载弯矩 Msp ： 当为挂车荷载时，应将轮重 P /2 改为 P /4 。 每米板宽的恒载弯矩为： 最后，悬臂根都一米板宽的最大弯矩 MS 为 MSp 与 MSg 按荷载组合原则组合而成。 ③ 铰接悬臂板最大剪力 a. 利用影响线进行计算 利用剪力影响线计算铰接悬臂板根部的剪力时，将车轮压力面的荷载尽量靠根部布置 ，旁边车轮压力面进入板跨内的长度为 0 ，则活载剪力 Q 为 ： ③ 铰接悬臂板最大剪力 b. 实用简化计算 每米板宽的恒载剪力为： 悬臂板根部每米板宽的最大剪力为： 活载产生的板的剪力为： （ 3 ）自由悬臂板的内力 ① 中梁 对于板边纵缝不相连的 自由悬臂板 ， 在计 算根部最大弯矩时，应将 车轮荷载靠板的边缘 布置 ， 此时 b = b 2 + H （ 无人行道一侧 ） 。 恒载弯矩、剪力计算方法与铰接悬臂板相同 。 1m 宽板条活载弯矩为 ： 1m 宽板条活载剪力为 ： ② 边梁外缘 （ 同学们可自行推导计算公式 ） 例 5-1 计算右图所示 T 形梁翼板所构成铰接悬臂板的设计内力。荷载为公路 —I 级。桥面铺装为 2 cm 的沥青混凝土面层容重 21 kN/m3 ，平均 9 cm 厚的 C25 混凝土垫层，其容重为 23 kN/m3 ， T 形梁翼板的容重为 25 kN/m3 ，试计算行车道板的设计内力。 1. 恒载及其内力 ( 以纵向 1m 宽的板条进行计算 ) (1) 每延米板上的恒载 g (2) 每米宽板条的恒载内力 2. 活载内力 本例按公路 —I 级车辆荷载计算内力。 (1) 每米宽板条的弯矩 用简化方法计算。将荷载对中布置在铰缝处，使铰剪力为零，按自由悬臂板计算。 (2) 每米宽板条的剪力 用简化方法计算。不考虑铰剪力的影响，按自由悬臂板计算，各板承担其上的荷载，则自由悬臂板根部的剪力： 3. 荷载组合 当桥面板按承载能力极限状态设计时，一般应采用基本组合，并根据现行 《 桥规 》(JTG D60-2004) 对相应荷载规定的荷载效应分项系数来求得计算内力。 本例均为恒载对结构物承载不利情况，其计算内力为 有了控制设计的计算内力，就可按钢筋混凝土板截面设计方法来设计板内的钢筋和进行相应的验算。 行车道板荷载 有效作用宽度的要点总结 1、 荷载有效分布宽度，同样适用于剪力计算。 2、 单向板 的有效工作宽度，靠近根部最小，靠 近跨中最大， 从根部到中部按 45 ° 线变化。 3、求 悬臂板 的弯矩 时，荷载最不利位置在铰处 （或边缘），但求的是根部弯矩。 4、考虑有效作用宽度，不能直接求荷载效应， 必须先把“力” 的 分布强度 求出，然后再在 每米宽 的板条范围内还原为“力”。 5.3 荷载横向分布计算 1 、结构自重内力 为了简化，将上部结构自重均摊给各主 梁。对于等截面梁桥，其结构自重是为 均布荷 载 。 梁内各截面 弯矩 M x 和 剪力 Q x 分别为 ： g 为简支梁 的荷载集度 2 、汽车、人群荷载内力 （ 1 ）荷载横向分布的基本概念 横向联结会使各主梁不同程度的参与工 作，并随着荷载作用位置 ( x ， y ) 的变化各主梁 承担的荷载也发生变化。 如图 ， 某主梁某一截面内力值为 S = P η 1 ( x ) η 2 ( y ) η 1 ( x ) —— 单梁在 x 轴方向某一截面的内力影响线 ； η 2 ( y ) —— 单位荷载沿横向 （ y 轴方向 ） 移动时 ， 某 梁所分配得的荷载比值变化曲线 ， 亦称 该梁的 荷载横向分布影响线 。 设荷载 P 作用于点 a ( x ， y ) 时 沿横向分配 给该主梁的荷载为 P' （ 如图 ） ，即 P' = P ∙ η 2 ( y ) 则按照 最不利位置布载 ，即可求得该梁所 受的最大荷载 P' max 。令 P' max = m ∙ P （ P 为轮轴重 ） 则称 m 为 荷载横向分布系数 ， 它表示某根 主梁所承担的各轴重的倍数 （ m 通常小于 1 ） 。 对于汽车、人群的 荷载横向分布系数 m 的计算公式如下所示： 汽车： 人群： ---- 对应于汽车和人群荷载集度的荷载 横向分布影响线竖标。 （ 2 ）荷载横向分布的计算 将空间计算问题转化成平面问题的做法只是一种近似的处理方法，因为实际上荷载沿横向通过桥面板和多根横隔梁向相邻主梁传递时情况是很复杂的，原来的集中荷载传至相邻梁的就不再是同一纵向位置的集中荷载了。但是，理论和试验研究指出，对于直线梁桥，当通过沿横向的挠度关系来确定荷载横向分布规律时，由此而引起的误差是很小的。 同一座桥梁内各根梁的荷载横向分布系数 m 是不相同的，不同类型的作用 ( 如汽车、人群荷载等 ) 其 m 值也各异，而且荷载在梁上沿纵向的位置对 m 也有影响。 图 5-21a 表示主梁与主梁间没有任何联系的结构，此时如中梁的跨中有集中力 P 作用，则全桥中只有直接承载的中梁受力，也就是说，该梁的横向分布系数 m =1 ，显然这种结构形式整体性差，而且是很不经济的。 图 5-21c 的情况，如果将各主梁相互间借横隔梁和桥面刚性连结起来，并且设想横隔梁的刚度接近无穷大 ，则在同样的荷载 P 作用下，由于横隔梁无弯曲变形，因此所有五根主梁将共同参与受力。此时五根主梁的挠度均相等，荷载 P 由五根梁均匀分担，每梁只承受 1/5P ，也就是说，各梁的横向分布系数 m =0.2 。 一般钢筋混凝土或预应力混凝土梁桥实际构造情况是，各根主梁虽通过横向结构联成整体，但是横向结构的刚度并非无穷大。因此，在相同的荷载 P 作用下，各根主梁将按照某种复杂的规律变形 ( 图 5-21b) ，此时中梁的挠度 ωb 必然要小于 ωa ，而大于 ωc ，设中梁所受的荷载为 mP ，则其横向分布系数 m 也必然小于 1 而大于 0.2 。 由此可见， 桥上荷载横向分布的规律与 结构的横向连结刚度 有着密切关系，横向连结刚度愈大，荷载横向分布作用愈显著，各主梁的负担也愈趋均匀。 （ 2 ）荷载横向分布的计算 求横向分布影响线有如下几种方法： 杠杆原理法 —— 把桥面板和横隔梁视作在主梁 上断开而简支在其上的 简支梁 偏心压力法 —— 把横隔梁视作一 刚性极大的梁 （ 又称 刚性横梁法 ） 铰接板 （ 梁 ） 法 —— 相邻板 （ 梁 ） 之间视为铰接 ， 只传递剪力 刚接梁 法 —— 相邻主梁之间视为刚接 比拟正交异性板法 —— 把主梁和横隔梁的刚度换算 成正交二向刚度不同的比拟弹性板求解 （ 2 ）荷载横向分布的计算 杠杆原理法 、 偏心压力法 、 铰接板 （ 梁 ） 法 刚接梁 法、 比拟正交异性板法 共同特点：从分析荷载在桥上的横向分布出发，求得各梁荷载横向分布影响线，从而通过横向最不利荷载来计算荷载横向分布系数 m 。有了作用于单梁上的最大荷载，就能按熟知的方法求得主梁的活载内力值。 钢筋混凝土和预应力混凝土梁桥的恒载一般比较大，即使在计算活载内力中会带来一些误差，然而对于主梁总的设计内力来说，这种误差的影响一般是不太大的。 ① 杠杆原理法 基本假定 忽略主梁之间的横向联系，假设 桥面板在主梁梁 肋处断开 ，而当作沿横向支承在主梁上的简支梁或悬 臂梁来考虑 （ 如图 。 注意： 边梁处不断开 ） 。 原理 当移动的单位荷载 P =1 作用于计算梁上时，该梁 承担的荷载为 1 ；当 P =1 作用于其他梁上时，该梁承担 的荷载为 0 ；该梁与相邻梁之间则按 线性变化 。 适用范围 杠杆原理法 适用于 计算 荷载靠近主梁支点 时的 荷 载横向分布系数 m o ， 也可用于 双主梁桥 。 ① 杠杆原理法 求解方法 为了求主梁所受的最大荷载，通常可利用反力影响线来进行，在此情况下，它也就是计算荷载横向分布系数的横向影响线。 有了各根主梁的荷载横向影响线，就可根据各种活载，如汽车和人群的最不利荷载位置求得相应的横向分布系数 moq 、 mor 。这里 m o 表示按杠杆原理法计算的荷载横向分布系数，拼音字母的脚标 q 和 r 相应表示汽车和人群荷载。 杠杆原理法计算荷载横向分布系数图示 【 例题 5-2 】 如图 ， 某五梁式钢砼 T 梁桥， 其桥面净空为 净 -7+2 ×0.75m 人行道。试求荷 载位于支点处时 1 号梁和 2 号梁相应于 公路 -II 级 汽车荷载和人群荷载 的横向分布系数。 【 例题 5-2 】 如图 ， 某五梁式钢砼 T 梁桥， 其桥面净空为 净 -7+2 ×0.75m 人行道。试求荷 载位于支点处时 1 号梁和 2 号梁相应于 公路 -II 级 汽车荷载和人群荷载 的横向分布系数。 【 解 】 荷载位于支点处，应用 杠杆原理法 计算 。 ① 绘制 1 、 2 号梁的荷载横向影响线 （ 如图 b 、 c ） ； ② 《 公路桥涵设计通用规范 》(JTG D60-2004) 规 定，在横向影响线上确定荷载沿横向最不利位 置。 公路 -II 级汽车荷载 ， 横向轮距为 1.8m ， 两 列汽车车轮横向最小间距为 1.3m ， 车轮距离人行 道缘石至少 0.5m （ 如图 b ） 。 杠杆原理法 例 5 ｜ 2 题图 ③ 求出相应荷载位置的影响线竖标值（各主梁影响线 在该梁处竖标值都为 1 ，同时按②的规定布置荷 载，解简单的 相似三角形 即可）。 ④ 由上述结果 （ 如图 ） ，可知 荷载横向分布系数 为： 汽车荷载： 2 号梁 ： 同理可得： 解毕 。 1 号梁 ： 人群荷载： ② 偏心压力法 （ 刚性横梁法 ） 在钢筋混凝土或预应力混凝土梁桥上，通常除在桥的两端设置横隔梁外，还在跨度中央，甚至还在跨度四分点处，设置中间横隔梁，这样可以显著增加桥梁的整体性，并加大横向结构的刚度。根据试验观测结果和理论分析可知，当设置了具有可靠横向联结的中间横隔，且在桥的宽跨比 的情况时 ( 一般称为窄桥 ) ，车辆荷载作用下中间横隔梁的弹性挠曲变形同主梁的相比微不足道。也就是说，中间横隔梁象一根刚度无穷大的刚性梁一样保持直线的形状。 从桥上受荷后各主梁的变形 ( 挠度 ) 规律来看，它完全类似于一般材料力学中杆件偏心受压的情况，这就是偏心压力法计算荷载横向分布的基本前提。鉴于横隔梁无限刚性的假定，此法也称“刚性横梁法”。 荷载 R i 与弹性挠度 w i 成正比 ② 偏心压力法 （ 刚性横梁法 ） 基本假定 1 ） 近似认为 中间横隔梁刚度无限大 ； 2 ） 忽略主梁的抗扭刚度。 原理 弹性范围内，某主梁所承受的 荷载 R i 与该荷载 所产生的跨中弹性 挠度 w i 成正比 。 横向偏心布置的荷 载作用下，靠近汽车一侧的边主梁受载最大。 适用范围 偏心压力法 适用于桥上 具有可靠联结 、 宽跨比 B/l ≤ 0.5 者 （ 窄桥 ） 计算 跨中截面荷载横向分布系数 m c 。 取跨中 x = l /2 截面 ，通常各主梁惯性矩 I i 相等。 偏 心荷载 P =1 可用 中心荷载 P =1 和 偏心力矩 M =1 ∙ e 来等 代，分别求出某主梁所承担的力 R i ' 和 R i " ，然后叠加 即得该梁沿横向分配的荷载 R i 。 1 ） 中心荷载 P =1 单独作用 因 I i 相等 ， 由挠度 w i ' = R i ' l 3 / 48 EI i 及 ∑ R i ' =1 知各 主梁荷载相等，为： 2 ） 偏心力矩 M =1 ∙ e 单独作用 在偏心力矩 M =1 ∙ e 作用下 ， 桥的横截面产生绕中 心点 O 的转角 θ ， 则各主梁跨中挠度为 w i " = a i tan θ ① 由力矩平衡条件，有 ∑ R i " ∙ a i =1 ∙ e ② 根据反力与挠度成正比的关系及 ① 式，有 R i " = Cw i " = C ∙ a i tan θ ③ 将 ③ 式代入 ② 式得 C ∙ tan θ ∙ ∑ a i 2 = 1 ∙ e ， 即 C ∙ tan θ = e / ∑ a i 2 ④ 将 ④ 式代入 ③ 式可得， 在偏心力矩作用下 i 号梁 的作用为： 右图为两 种情况单独作 用下的主梁变 形 、 反力图 示 。 3 ） 总作用 在偏心单位荷载作用下， i 号梁的作用为： 这就是 i 号梁的荷载影响线在各梁位处的竖标值。 当荷载位置 e 和梁位 ai 位于形心轴同侧时，取正号，反之取负号。 4 ） 当 P=1 位于 k 号梁上时（ e=a k ） i 号梁的作用为： 5 ） 当主梁的惯性矩 I i 不相等时 【 例题 】 计算跨径 l =19.50m 的简支梁，尺寸 如 图 。求荷载在跨中时 1 号边梁的 荷载横向分布系数 。 【 例题 】 计算跨径 l =19.50m 的简支梁，尺寸 如 图 。求荷载在跨中时 1 号边梁的 荷载横向分布系数 。 1 ） 求横向荷载分布影响线竖标 本 桥各主梁的横截面相同，梁数 n =5 ，梁间距为 1.60 m ，则 【 解 】 设 横隔梁刚度很大。其承重结构宽跨比为： 故可按 偏心压力法 计算横向分布系数 m c 。 2 ） 绘制荷载横向分布影响线并布置最不利荷载 1 号梁在两边梁处的 横向影响线竖标值 为： 解得 e =1.6m ，且在 1 号梁异侧， 即 4 号梁处为零。 由图知人行道缘石至 1 号梁轴的距离为 0.3m 。设 偏心距为 e 时， 1 号梁横向分布影响线竖标为零： 求影响线 的零点 同侧 + 异侧 − 据此，解相似三角形即可算出荷载最不利布置 时各荷载点的影响线竖标 η qi 和 η r （ 如图 ） 。 【 作业 】 用 偏心压力法 求 2 号梁和 3 号梁的荷载横向分 布系数。 解毕 。 3 ） 计算荷载横向分布系数 m c 1 号梁的活载横向分布系数分别计算如下： ③ 修正 偏心压力法 （ 考虑主梁的抗扭刚度 ） 刚性横梁法假设横隔梁绝对刚性，同时忽略了主 梁的抗扭刚度 （ 即不计主梁扭矩抵抗活荷载的贡献 ） ， 导 致边梁的 受力偏大 。 为了弥补此方法的不足，国内外 广泛采用 考虑抗扭刚度的 修正刚性横梁法 。 力偶矩 M =1 ∙ e 的 作用，引起各片主梁的竖向位 移，由于截面的转动，各片主梁不仅会产生 竖向挠 度 ，而且还必然同时引起 扭转 （ 如图 ） 。由此可见， 要计入主梁抗扭的影响，需对不考虑抗扭的情况给以 修正。 主梁在力偶作用下的受力与变形 如图， 取 跨中截面 来分析。在 M =1 ∙ e 作用 下，各片主梁除产生不同的 挠度 w i " 外，尚有 一个相同的 转角 θ 。各主梁对横隔梁的 竖向反 力 R i " 和 抗扭矩 M Ti 满足如下平衡条件： 由 材料力学 ， 竖向力 R i " 与 挠度 w i " 和截面 扭矩 M Ti 与 扭转角 θ 的关系分别为： ① ② 根据小变形原理，由 图 和 ② 式可知： ③ 由 ③ 式，可得 k 号梁 与 i 号梁 的荷载关系为 ： ④ 将 ③ 式 代入 ② 式，可得 ： ⑤ 将 ④ 式 与 ⑤ 式联立，可得 ： ⑥ 将 ④ 式 和 ⑥ 式代入 ① 式，有 ： 即 ⑦ 化解 ⑦ 式并整理，得 k 号梁 的荷载为 ： 用 i 代 k ，即有 于是， i 号梁所承担的 总荷载 为： 当各主梁截面相同时，有 I i = I ， I Ti = I T ，则 当主梁间距相同时，可令： n —— 主梁根数 ； B —— 桥宽 ； ξ —— 与主梁根数有关的系数见 下表 。 此时有： 从 上 式中可以看出， l /B 愈大的桥，抗扭刚度对 横向分布系数的影响也愈大。 n 4 5 6 7 ξ 1.067 1.042 1.028 1.021 计算时， 砼的剪切模量 G ≈ 0.4 E ； T 形 或 工字 形梁 ，其 抗扭惯矩 I T 约等于各个矩形截面 I Tj 之和： 式中各符号的意义 见右图； c 值可查下表。 t/b 1 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 ＜ 0.1 c 0.141 0.155 0.171 0.189 0.209 0.229 0.250 0.270 0.291 0.312 1/3 （例题） 计算跨径 l =19.50m 的简支梁桥，其横截面如图 5-27a 所示。考虑主梁抗扭刚度，求荷载位于跨中时 1 号边梁的荷载横向分布系数 mcq ( 汽车荷载 ) 和 mcr ( 人群荷载 ) 。 T 形主梁的细部尺寸如图 5-27c 所示。 1. 计算 I 和 I T 1. 计算 I 和了 I T 2. 计算抗扭修正系数 β 3. 计算横向影响线竖标值 4. 计算荷载横向分布系数 横向分布系数计算图示 5.3.6 荷载横向分布系数沿桥跨的变化 荷载位于桥跨中间部分时，由于桥梁横向结构 ( 桥面板和横隔梁 ) 的传力作用，使所有主梁都参与受力，因此荷载的横向分布比较均匀。但当荷载在支点处作用在某主梁上时，如果不考虑支座弹性变形的影响，荷载就直接由该主梁传至支座，其它主梁基本上不参与受力。因此，荷载在桥跨纵向的位置不同，对某一主梁产生的横向分布系数也各异。 5.3.6 荷载横向分布系数沿桥跨的变化 要精确计算 m 值沿桥跨的连续变化规律是相当冗繁的，而且也会使内力计算更麻烦。 1. 对于无中间横隔梁或仅有一根中横隔梁的情况，跨中部分采用不变的 mc ，从离支点 l /4 处起至支点的区段内 m 呈直线形过渡 ( 图 5-47a) 。 5.3.6 荷载横向分布系数沿桥跨的变化 2. 对于有多根内横隔梁的情况， mc 从第一根内横隔梁起向 m0 直线形过渡 ( 图 5-47b) 。 这样，主梁上的活载因其纵向位置不同，就应有不同的横向分布系数。图中 mo 可能大于 mc ，也可能小于 mc ，如图 5-47 所示。 杠杆原理法 5.3.6 荷载横向分布系数沿桥跨的变化 ① 对于弯矩 由于跨中截面车轮加载值占总荷载的绝大多数， 可近似认为其它截面的横向分布系数与跨中相同； 其它截面一般也可取不变的 m c ，但 中梁 的 m o 、 m c 差距较大 （ 尤其在横梁少于 3 根时 ） ， 宜考虑沿跨径 变化 。 其他位置 确定 支点 位置的荷载横向分布系数 m o 偏心压力法 确定 跨中 位置的荷载横向分布系数 m c ？ ② 对于剪力 近似影响面与实际情况相差较大。在计算 梁端截 面最大剪力 时，应考虑荷载横向分布系数 沿桥跨的变 化 （ 如图 ） 。 5.4 主梁内力计算 主梁的内力计算，可分为运营和施工两个阶段的内力计算。本节主要介绍运营阶段内力计算。 根据作用于一片主梁的恒载和通过横向分布系数求得的计算活载，就可按一般工程力学的方法计算主梁的截面内力 ( 弯矩 M 和剪力 Q ) 。有了截面内力，就可按钢筋混凝土和预应力混凝土结构的设计原理进行主梁各截面的配筋设计或验算其强度及应力等。 5.4 主梁内力计算 小跨径的简支梁 只需计算跨中截面的最大弯矩和支点截面及跨中截面的剪力。跨中及支座之间各截面的剪力可以近似地按直线规律变化，弯矩可假设按二次抛物线规律变化 较大跨径的简支梁 还应计算跨径 1/4 截面的弯矩和剪力。如果主梁沿桥轴方向截面有变化，则还应计算截面变化处的内力。 5.4.1 恒载内力的计算 主梁恒载内力包括主梁自重 ( 前期恒载 ) 引起的主梁自重内力 S G 1 和后期恒载 ( 如桥面铺装、人行道、栏杆、灯柱等 ) 引起的主梁后期恒载内力 S G 2 。 主梁为等截面 它承受沿跨长的均布荷载 g ，其截面恒载内力可用均布荷载 g 乘上所欲计算内力的影响线总面积。当然也可以用分析的方法来计算各截面的内力。 主梁为变截面 需要按沿梁长变化的恒载集度 gx 来计算各截面的内力，在一般恒载集度变化情况下，利用影响线计算恒载内力较为方便，其截面恒载内力可按下式计算 当影响线或荷载集度为线性时，上述积分可方便地用图乘法求出。 5.4.1 恒载内力的计算 确定恒载集度 为简化起见，可将沿桥跨分点作用的横隔梁重量、沿桥横向不等分布的铺装层重量以于作用于两侧的人行道和栏杆等重量均匀分布地分摊给各主梁承受。因此，对于等截面梁桥的主梁，其计算恒载是简单的均布恒载。为了精确起见，也可恨据施工安装的情况，将人行道、栏杆、灯柱和管道等重量象活载计算那样，按荷载横向分布的规律进行分配。 组合式梁桥 按实际施工组合情况，分阶段计算恒载内力。 预应力混凝土简支梁桥 在施加预应力阶段，往往要利用梁体自重 ( 前期恒载 ) 来抵消强大预应力钢筋 ( 钢绞线 ) 张拉力在梁体上翼缘产生的拉应力。在此情况下，也要将恒载分成两个阶段 ( 即前期恒载和后期恒载 ) 来进行分析。在特殊情况下，恒载可能要分成更多的阶段来考虑。 5.4.1 恒载内力的计算 确定了 恒载集度 g 之后 ，利用内力影响线和下列公式计算梁内各截面的弯矩 M 和剪力 Q ，当恒载分阶段计算时，应按各阶段的计算恒载集度 g ，来计算内力，以便进行内力或应力组合。 例题： 计算例 5-6 中图 5-43 所示的五梁式装配式钢筋混凝土简支梁桥主梁的恒载内力；每侧的栏杆及人行道构件重量的作用力为 5kN/m 。 1. 恒载集度 2. 永久荷载内力 计算边主梁的弯矩和剪力，用 《 材料力学 》 公式计算，计算图式如图 5-48 所示。 恒载内力计算图式 5.4.1 活载内力的计算 主梁活载内力由基本可变荷载中的车辆荷载和人群荷载产生。 主梁活载内力计算分为两步：第一步求某一主梁的最不利荷载横向分布系数 m ；第二步应用主梁内力影响线，将荷载乘以荷载横向分布系数后，在纵向按最不利位置在内力影响线上加载，求得主梁最大活载内力。根据规范要求，主梁采用车道荷载及人群荷载布载，应将其均布荷载和集中荷载引起的内力进行叠加，求得总效应，同时对汽车荷载还必须考虑冲击力的影响。 汽车、人群荷载效应计算 均布荷载 应布置于同号影响线内 集中荷载 应布置于影响线峰值处 荷载横向分布系数 主梁内力影响线 车道荷载 截面内力 截面上汽车、人群荷载 作用效应 一般公式为： ② 支点 、 近支点处截面的剪力效应 ① 跨中范围内截面的弯矩、剪力效应 各重要符号意义见下页。 S k —— 截面的弯矩或剪力标准值 M k 、 Q k ； μ —— 汽车荷载的冲击系数 ； ξ —— 汽车荷载横向折减系数 （ 表 1-3-5 ， 教 P34 ） ； q k —— 车道荷载中均布荷载标准值 ； Ω —— 弯矩 、 剪力影响线面积 ； m c —— 跨中横向分布系数 ； m o —— 支点处横向分布系数 ； m i —— 沿桥跨纵向与集中荷载位置对应的横向分布系数 ； P k —— 车道荷载中集中荷载标准值 ； y i —— 沿桥跨纵向与集中荷载位置对应的内力影响线竖标值 ； q r —— 沿桥跨纵向的人群荷载标准值 ； Ω Q —— 剪力影响线面积 ； a —— 沿桥跨纵向的荷载横向分布系数 m 过渡段长度 ； —— m 变化区荷载重心处对应的剪力影响线竖标值 ； y Q max —— 剪力影响线峰值处竖标 。 例题： 例 5-6 中图 5-43 所示的五梁式简支梁桥，桥梁基频为 4.12Hz ，人群荷载标准值为 3 kN/m2 ，试计算 1 号梁和 3 号梁在公路 —I 级车辆荷载、车道荷载和人群荷载作用下的内力。 1. 荷载横向分布系数 2. 主梁跨中截面弯矩 正如前面所述，在计算主梁弯矩时，对跨中的荷载横向分布系数与跨内其他各点上的荷载横向分布系数是采用相同的值，这是实用方法基本原理的前提所决定的。目前在实用计算中，全跨采用同一的跨中荷载横向分布系数 mc 。图 5-49 为简支梁跨中截面弯矩影响线和设计荷载的最不利布置图。 ξ =1 (1) 1 号梁跨中截面弯矩 (2) 3 号梁的跨中弯矩 3. 主梁跨端截面剪力 1 号梁跨端的设汁荷载剪力计算；图 5-50a 为主梁纵断面图，图 5-50b 为荷载横向分布系数沿跨长分布图；图 5-50c 为跨端截面剪力影响线图。 人群荷载 图 5-51 所示为人群荷载作用下支点剪力的荷载横向分布系数沿跨长分布图以及剪力影响线。 5.5 横隔梁内力计算 计算方法 求计算荷载时用 杠杆原理法 求截面内力时按 弹性支承连续梁 受力特点 弹性地基梁 研究对象 跨中横隔梁 （ 受力最大 ） 1 、横隔梁上的计算荷载 横隔梁的计算荷载图示 假设荷载在相邻横隔梁之间按 杠杆原理法 分布 （ 如图 ）。 因而纵向一列汽车 车道荷载 轮重分布给跨 中横隔梁的 计算荷载 为： 人群荷载满布于同号影响线上，则： Ω —— 按杠杆原理计算的纵向荷载影响线面积 ； l a —— 弯矩 、 剪力影响线面积 ； y 1 —— P k 所对应的纵向荷载影响线竖标 ， y 1 =1 。 2 、横隔梁的内力影响线 取 r – r 左侧隔离体。 当 P 在 r – r 左侧时： 当 P 在 r – r 右侧时： M r 、 Q r —— 横隔梁 r – r 截面的弯矩 、 剪力 ； e —— 荷载 P =1 至 r – r 截面的距离 ； b i —— 支承反力 R i 至 r – r 截面的距离 。 然后利用支座反力（即主梁承担的荷载） R i 的横 向分布影响线求横隔梁某 截面内力的影响线。 3 、横隔梁内力计算 在横隔梁计算截面的内力影响线上按最不利布 载，求出该截面上的荷载效应 。 【 例题 2-4-7 】 计算 【 例题 2-4-5】 中所示装配式钢砼简 支梁桥跨中横隔梁在 ②、③ 号主梁之间 r – r 截面上的弯矩 和靠近 ①号边主梁处截面 r o – r o 上的剪力 （ 公路 - Ⅱ 级 ） 。 【 解 】 1 ） 公路 - Ⅱ 级 ① 确定作用于中横隔梁上的计算荷载 跨中横隔梁的最不利布载 如图 所示，则纵向一列车 轮对于中横隔梁的 计算荷载 为 ： ② 绘制中横隔梁 r – r 截面弯矩 M r 的影响线 用 偏心压力法 绘出 ①、②号梁的荷载横向分布影 响线 （ 如图 a ） ，再计算 r – r 截面 内力影响线 。 中横隔梁内力影响线 M r 的 影响线竖标值计算如下 （ 运用 公式 ） ： P =1 作用在 ① 号梁轴上时， R 11 =0.60 ， R 21 =0.40 ，有 P =1 作用在 ② 号梁轴上时， R 12 =0.40 ， R 22 =0.30 ，有 P =1 作用在 ⑤ 号梁轴上时， R 15 = − 0.20 ， R 25 =0 ，有 M r 的 影响线在 r – r 截面为 折线变化 处 ，将 η M r1 =−0.64 和 η M r2 =0.40 的连线延伸至 r – r 截面得交点 η M rr =0.92 ，再将 η M rr 与 η M r5 =−0.48 相连即可绘出 M r 的 影响线 （ 如图 b ） 。 ③ 绘制中横隔梁 r o – r o 截面的剪力影响线 P =1 作用在 r o – r o 截面以左 时 ， 有 P =1 作用在 r o – r o 截面以右时 ， 有 靠近 ①号边主梁处截面 r o – r o 上 （ 如图 ） 的剪力 影响线可计算如下： 将 R 11 、 R 15 代入则分别有 可绘成 影响线 （ 如图 c ） 。 ④ 截面内力计算 （ 在影响线上按最不利布载 ） 2 ） 人群荷载 由横隔梁内力影响线 图 a ）、 b ） 可知： ◆ 人群荷载总在影响线负号区域内 ◆ 引起的内力与汽车引起的内力反号 ◆ 引起的内力绝对值远比汽车小 所以，不必布置人群荷载 （ 否则反而使横隔梁截 面内力减小 ） 。 3 ） 内力组合 分别按 承载能力极限状态 和 正常使用极限状态 （ 不计冲击 ） 进行组合 （ 教材 P 45 、 P 46 ） 。 【 注 】 横隔梁自重集度较小 ， 且全跨满布 ， 而内力影 响线有正有负 ， 所以自重内力甚小 ， 计算时可忽略 。 桥梁设计必须验算梁的 变形 （ 挠度 ），以确保 结构具有足够的 刚度 。 钢筋混凝土及预应力混凝土简支梁 长期挠度值 f c 按下式计算： f c 、 f —— 长期挠度值 、 短期挠度值 ； η θ —— 挠度长期增长系数 ： C40 以下混凝土取 1.60 ， C45 ~ C80 混凝土取 1.45 ~ 1.35 ， 其 余按线性插值 ； 计算预应力混凝土简支梁 的预加反拱值时取 2.0 。 5.6 主梁变形和裂缝验算 钢筋混凝土简支梁的短期挠度值 f 按下 式计算： M S —— 由荷载短期效应组合的弯矩值 ； l —— 计算跨径 ； B —— 开裂构件等效截面抗弯刚度 ； B 0 —— 全截面抗弯刚度 ， B 0 =0.95 E c I 0 ； B cr —— 开裂截面抗弯刚度 ， B cr = E c I cr ； M cr —— 开裂弯矩 ， 对预应力 M cr =( σ pc + γ f tk ) W 0 ； I 0 —— 全截面换算截面惯性矩 ； I cr —— 开裂截面换算截面惯性矩 ； γ —— 受拉区混凝土塑性影响系数 ， γ =2 S 0 / W 0 ； S 0 —— 全截面换算截面重心一侧对重心面积矩 ； f tk —— 混凝土轴心抗拉强度标准值 ； W 0 —— 换算截面抗裂边缘的弹性抵抗矩 。 《 桥规 》 规定，验算 主梁变形 时，不计入结构 自重产生的长期挠度，不计入汽车冲击力： 《 桥规 》 规定， 预拱值 通常按结构自重和一半 可变荷载频遇值计算的长期挠度之和： 《 桥规 》 规定，当由结构自重和可变荷载所计 算的长期挠度不超过 1/1600 时，可不设预拱度。 ③ 铰接板（梁）法 现浇混凝土纵向企口缝连结的装配式板桥以及仅在翼扳间用焊接钢板或伸出交叉钢筋连结的无中间横隔梁的装配式桥，由于块件间横向具有一定的连结构造，但其连结刚性又很薄弱，因此对于跨中荷载横向分布的计算，上面所述的 “ 杠杆原理法 ” 和 “ 偏心压力法 ” 均不适用。 。 鉴于这类结构的受力状态实际接近于数根并列而相互间横向铰接的狭长板 ( 梁 ) ，故对此专门拟定了横向铰接板 ( 梁 ) 理论来计算荷载的横向分布。 ③ 铰接板（梁）法 基本假定 1 ） 板块之间的铰仅传递竖向剪力，横向弯矩、 纵向剪力和法向力 ； 2 ） 作用在桥跨上的集中荷载，近似地用沿桥跨连续分布的正弦等效荷载来代替； 3 ） 略去泊松比的影响。 ③ 铰接板（梁）法 横向分布影响线 当单位集中力作用于板块上时，同样可以用一个等效正弦荷载来代替，取跨径中央峰值处一单位长度的横向板带来分析， 单位力峰值 P =1 作用于板块 1 上时，每个铰接处将产生一对竖向剪力 Qi 将单位力 P =1 分布到各块板上。各块板受到的力为： 按比例描绘在 1 ～ 5 块板的下面，以光滑的曲线连接，若结构形式、支承条件、材料性质等均不发生改变时，按变位互等定理知其即为板块 1 的横向分布影响线。 ③ 铰接板（梁）法 基本假定 1 ） 近似认为 中间横隔梁刚度无限大 ； 2 ） 忽略主梁的抗扭刚度。 原理 弹性范围内，某主梁所承受的 荷载 R i 与该荷载 所产生的跨中弹性 挠度 w i 成正比 。 横向偏心布置的荷 载作用下，靠近汽车一侧的边主梁受载最大。 适用范围 偏心压力法 适用于桥上 具有可靠联结 、 宽跨比 B/l ≤ 0.5 者 （ 窄桥 ） 计算 跨中截面荷载横向分布系数 m c 。 【 例题 】 如图：计 算跨径 l =19.5m的桥梁横截 面如 右 图所示 。 试求荷载 位于跨中时1号、2号梁的 荷载横向分布系数 m cq 和人 群荷载分布系数 m cr 。 【 解 】 荷载在跨中，用 修正刚性横梁法 计算 。 1 ） 计算 I 和 I T 翼板 换算厚度 为 则 确定主 梁截面 重心的位置 a x : 主梁抗弯惯矩 I ： 主梁抗扭惯矩 I T ： 则 对翼板 t 1 /b 1 = 0.12/1.6=0.075<0.1 ， 查表得 c 1 =1/3 ； 对 梁肋 t 2 /b 2 = 0.18/1.18=0.152 ， 查表得 c 2 =0.301 。 2 ） 计算抗扭修正系数 β 已知 n = 5时 ， ξ =1.042 ，又 G = 0.4 E ， 代入下式 ： 3 ） 计算横向影响线竖标值 （ 后续同前例题 ） 及 注意比较 【 例题 2-4-6】 仍以 前述五梁式装配式钢砼简支梁桥 为例。试求 ① 号边主梁在公路 - Ⅱ 级和人群荷载作用下 的跨中最大弯矩、最大剪力及支点处的最大剪力。 【 解 】 对已计算出的数据，汇总于表中。 1 ） 荷载横向分布系数 m 的计算 梁号 荷载位置 公路 - Ⅱ 级 人群荷载 计算方法 ① 号 边主梁 跨中 m c 0.538 0.684 偏心压力法 支点 m o 0.438 1.422 杠杆原理法 【 注 】 由表中数据 ， 根据横向分布系数沿桥跨纵向变 化规律可作出 ① 号边主梁 m 沿纵跨分布图 。 2 ） 均布荷载 q k 、 q r 和内力影响线面积 Ω 的计算 截面 q k (kN/m) q r (kN/m) Ω (m 2 ， m) 影响线图示 M l/2 公路 - Ⅱ 级 10. 5 ×0.75 = 7.875 3. 0 ×0.75 = 2.25 Ω = l 2 /8 =19. 5 2 /8 = 47. 53 m 2 Q l/2 7.875 2.25 Ω =1/2 × 1/2 × 19. 5 × 1/2 = 2. 44 m Q 0 7.875 2.25 Ω =1/2 × 19. 5/2 = 9. 75 m 3 ） 公路 - Ⅱ 级集中荷载 P k 的计算 计算弯矩效应时 计算剪力效应时 4 ） 汽车 冲击系数 μ 的计算 A =0.4044 m 2 G = 0.4044× 25 =10.11 kN/m m c = G/g = 10.11/9.81 =1.0306 kN ∙ s 2 /m 2 I c =6748200 cm 4 =0.067482 m 4 C 30 砼弹性模量取 E = 30 k N/mm 2 = 3 .0 ×1 0 10 N/m 2 ， 简支梁桥基频 f 为 则 1+ μ = 1.295 冲击系数 μ 截面 荷载 类型 q k 或 q r (kN/m) P k (kN) 1+ μ m c Ω 或 y (m 2 ,m) S (kN ∙ m,kN) S i S M l/2 公路 Ⅱ 级 7.875 178.5 1.295 0.538 47.53 260.78 867.05 4.875 606.27 人群 2.25 — — 0.684 47.53 73.15 Q l/2 公路 Ⅱ 级 7.875 214.2 1.295 0.538 2.438 13.38 88.00 0.5 74.62 人群 2.25 — — 0.684 2.438 3.75 5 ） 跨中弯矩 M l/2 、 跨中剪力 Q l/2 的计算 双车道不折减，即 ξ =1 。 计算过程见下表。 6 ） 支点截面剪力 Q ok 的计算 绘出 横向分布系数变化 图及支点剪力影响线。 横向分布系数变化区段的长度为 a =4.9m ，则 m 变 化区荷载重心处的剪力影响线竖标为： 汽车荷载作用下 支点截面最大剪力 Q oqk 为 人群荷载作用下 支点截面最大剪力 Q ork 为 序号 荷载类别 弯矩 M （ kN ∙ m ） 剪力 Q （ kN ） 梁端 梁端 跨中 ① 结构自重 0 156.59 0 ② 汽车荷载 0 172.70 88.00 ③ 人群荷载 0 18.73 3.75 ④ S ud =1.2 ① +1.4② +0.8 ×1.4 ③ 0 M oud 450.67 Q oud 127.40 Q l / 2 ud 跨中 763.35 867.05 73.15 2211.82 M l / 2 ud 7 ） 荷载组合 （ 承载力极限状态 ）